Sobald Licht von einem Ausbreitungsmedium bestimmter optischer Dichte in ein anderes Medium mit anderer Dichte übertritt, wird es von seiner Ausbreitungsrichtung abgelenkt. Man spricht von Brechung oder Refraktion. Weil die Ablenkung zusätzlich von der Wellenlänge des Lichts abhängt, wird weisses Licht dadurch in seine einzelnen Spektralbereiche aufgeteilt; es entsteht ein farbiges Spektrum. Unsere vorliegende Folge widmet sich den Auswirkungen dieses Phänomens innerhalb der Fotografie.
Refraktion
Dringt ein Lichtstrahl schräg in die glatte Fläche eines durchsichtigen Körpers, wird ein geringer Teil gesetzmässig reflektiert (Teilreflexion). Der Hauptteil jedoch erfährt eine Ablenkung in der geradlinigen Ausbreitungsrichtung, er wird gebrochen.
Die Gründe für diese Ablenkung sind in einem Geschwindigkeitsunterschied zu suchen. Die Ausbreitungsgeschwindigkeit der elektromagnetischen Strahlung Licht beträgt im luftleeren Raum rund 300’000 km pro Sekunde. Sobald sich Licht dagegen in einem optisch dichteren Medium – wie zum Beispiel Wasser oder Glas – ausbreitet, ist seine Geschwindigkeit merklich geringer. So beträgt die Lichtgeschwindigkeit im Medium Wasser nur noch rund 225’000 km pro Sekunde oder in einem Diamanten sogar nur 125’000 Sekundenkilometer.
Tritt Licht zum Beispiel vom Medium Luft schräg in die Oberfläche von Wasser ein, erleidet der Lichtstrahl einen gewaltigen Geschwindigkeitsverlust; es tritt Refraktion oder Lichtbrechung ein.
links: Refraktion des Lichts mit Teilreflexion an der Grenzfläche
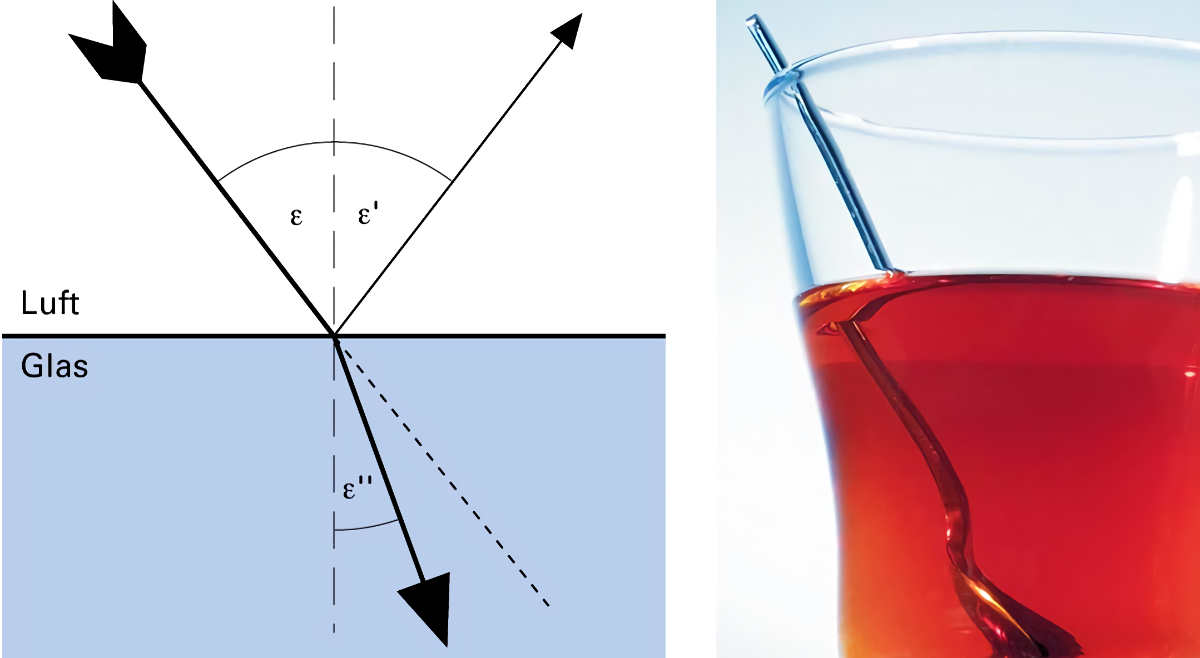
rechts: Das alltäglich zu beobachtende Phänomen des optisch geknickten oder unterbrochenen Löffels im Teeglas oder der entsprechend geknickte Stab, wenn man ein gerades Stück Holz ins Aquarium taucht, sind praktische Beweise für die unterschiedliche Ausbreitungsgeschwindigkeit.
Ein Gedankenexperiment macht das optische Gesetz verständlich: Stellen wir uns eine in Viererkolonne marschierende Truppe vor, die in normaler Marschgeschwindigkeit auf einer Betonpiste einhergeht. Im gleichen Moment, in dem die Spitze der Truppe am Ende der Piste in sumpfigen Morast gerät, wird die «Marschgeschwindigkeit» plötzlich kleiner. Verläuft die Grenze zwischen Betonpiste und Morast schräg zur Marschrichtung, wird nicht das gesamte erste Glied gleichzeitig langsamer, sondern Mann um Mann, es entsteht ein entsprechender Schwenk. Das Experiment ist natürlich auch umkehrbar. Tritt die marschierende Truppe schräg aus dem Morast auf die glatte Fläche, erhöht sich die Marschgeschwindigkeit wieder. Aus den gleichen Gründen entsteht ein erneuter Schwenk, diesmal aber in die andere Richtung.
Richtungsschwenk an einer Grenzfläche
Brechungsgesetz und Brechungsindex (Brechzahl) n
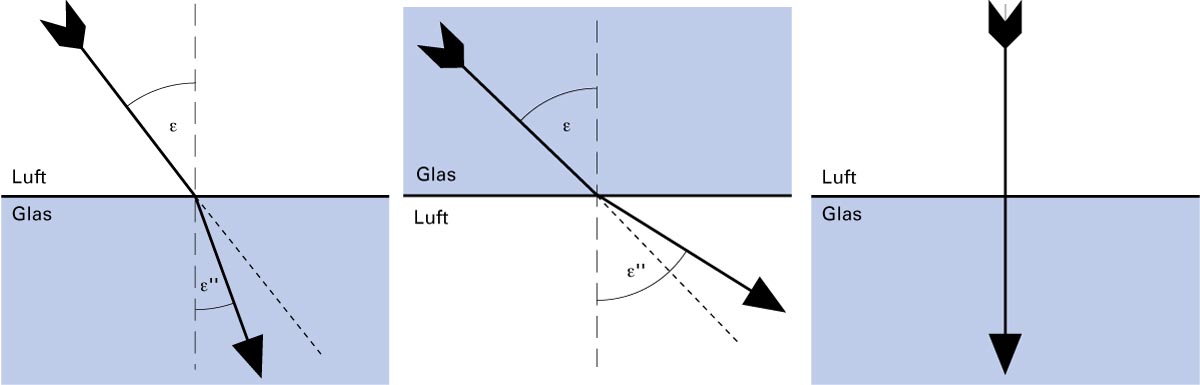
links: 1. Brechungsgesetz: Tritt ein Lichtstrahl von einem optisch dünnen in ein optisch dichteres Medium, so wird er dem Lot zugebrochen. Der Brechungswinkel εʹʹ ist kleiner als der Einfallswinkel ε.
Mitte: 2. Brechungsgesetz: Tritt ein Lichtstrahl von einem optisch dichteren in ein optisch dünneres Medium, so wird er vom Lot weg gebrochen. Der Brechungswinkel εʹʹ ist grösser als der Einfallswinkel ε.
rechts: 3. Brechungsgesetz: Tritt ein Lichtstrahl senkrecht auf eine Grenzfläche, erfährt er keine Ablenkung. Der Brechungswinkel εʹʹ ist gleich dem Einfallswinkel ε, nämlich beide 0°.
Die Brechzahl n ist eine Materialkonstante, die für die Ausbreitung einer Lichtwelle in dem betreffenden Stoff massgeblich ist.
Vakuum n = 1,00000 (300’000)
Luft n = 1,00028 (299’916)
Wasser n = 1,33 (225’000)
Alkohol n = 1,362 (220’264)
Kronglas n = 1,51 (197’000)
Flintglas n = 1,79 (167’000)
Diamant n = 2,4 (125’000)
In Klammern: Lichtgeschwindigkeit in km pro Sekunde
Sie ist definiert als das Verhältnis der Lichtgeschwindigkeit im Vakuum (C0) zur Lichtgeschwindigkeit im betreffenden Medium (Cmed). Die Ausbreitungsgeschwindigkeit in einem Medium dichter als Vakuum ist zudem von der Wellenlänge λ (Delta) abhängig.
Die Brechzahlen zweier Medien A und B verhalten sich umgekehrt wie die Ausbreitungsgeschwindigkeit des Lichts in ihnen:
Das Verhältnis nB : nA bezeichnet man als Brechungsverhältnis. Nach dem Snelliusschen Brechungsgesetz gilt folgende Gleichung:
Ist das Medium A Vakuum oder annähernd Luft (Brechzahl 1), vereinfacht sich das Gesetz:
Der Brechungsindex (Brechzahl) ist im Weiteren von der Wellenlänge des Lichts abhängig. Normalerweise gibt man den mittleren Brechungsindex (nd) an, der Gültigkeit hat für die Natrium-Linie, das heisst eine Wellenlänge von 587,6 nm, bei welcher die Empfindlichkeit des menschlichen Auges am grössten ist.
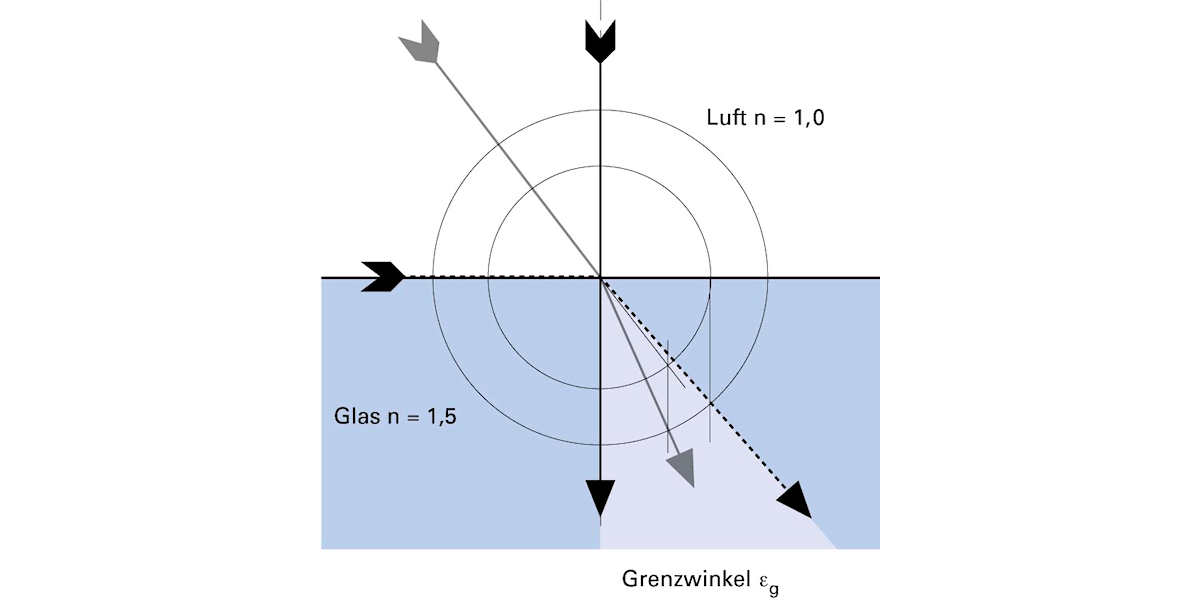
Grenzwinkel
Konstruiert man die Brechung für verschiedene Einfallswinkel, wenn ein Lichtstrahl von einem dünnen in ein optisch dichteres Medium eintritt, stellt man eine verblüffende Tatsache fest:
Der Strahl mit Einfallswinkel 0° ändert beim Eintritt ins dichtere Medium seine Ausbreitungsrichtung nicht. Für jeden anderen einfallenden Strahl können wir gemäss den Konstruktionsbestimmungen (zwei Kreisbögen, deren Radien sich wie die beiden Brechungsindizes verhalten) die Brechung bestimmen. So auch für einen Einfallsstrahl, der praktisch an der Oberfläche der Grenzfläche entlangstreicht, der also einen Einfallswinkel von 90° (oder, um Ihnen den Denkvorgang zu vereinfachen, nahezu 90°) aufweist. In der Konstruktion führen wir den Strahl geradlinig weiter bis zum ersten Kreisbogen, gehen von dort parallel dem Lot bis zum zweiten Bogen und erhalten so die Lage des gebrochenen Strahls.
Ändert sich der Einfallswinkel von 0° bis 90°, so ändert sich im optisch dichteren Medium der Brechungswinkel von 0° bis zu einem Winkel, der kleiner als 90° ist, dem sogenannten Grenzwinkel. Oder anders gesagt, ein eintretendes konvergentes Bündel mit der Öffnung 90° konzentriert sich im dichteren Medium zu einem Bündel mit geringerer Öffnung.
Die Grösse des Grenzwinkels ist vom Brechungsverhältnis der beiden beteiligten Medien abhängig.
Ist nA = 1 (annähernd Luft), so sind die Grenzwinkel für
Wasser ~ 48°
Alkohol ~ 47°
Kronglas ~ 41°
Flintglas ~ 34°
Diamant ~ 24°
Wenn Sie sich das Prinzip des Grenzwinkels veranschaulichen, erkennen Sie, dass ein Aquariumfisch nur dann die Möglichkeit hat, aus seinem Gefängnis hinauszuschauen, wenn seine Blickrichtung sich innerhalb des Grenzwinkels befindet. Ausserhalb dieses Winkels erscheint ihm die Aquariumwand wie ein vollständig reflektierender Spiegel. Sie können dies leicht nachprüfen, wenn Sie sich das nächste Mal im Schwimmbad befinden: Tauchen Sie im Schwimmbecken bis auf den Grund und betrachten Sie – den Blick nach oben gerichtet – Ihre Mitschwimmer. Ist Ihre Blickrichtung zum Lot, so vermögen Sie durchs Wasser die Köpfe der Schwimmer zu sehen. Befinden Sie sich aber näher an der Wasseroberfläche, so sehen Sie lauter kopflose Menschen. Ausserhalb des Grenzwinkels von 48° können Sie nicht aus dem Wasser hinaus sehen!
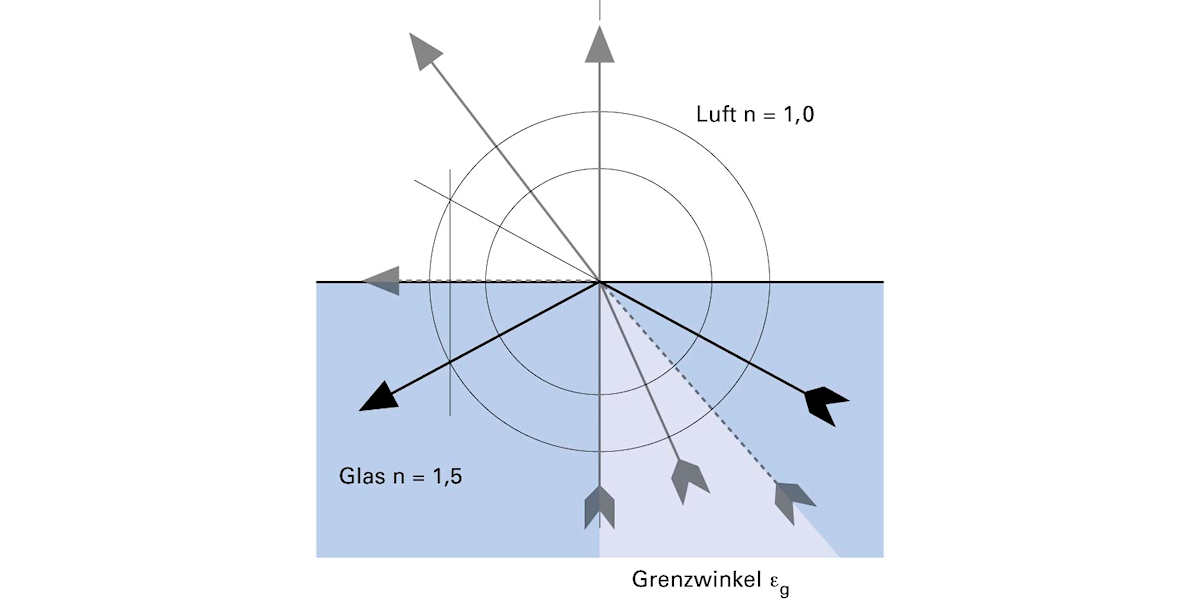
Totalreflexion
Ein Strahl, der vom dichteren in ein dünneres Medium austreten will, kann dies nur innerhalb des Grenzwinkels tun. Ist der Ausfallswinkel eines Strahls grösser als der Grenzwinkel, kann der Strahl das Medium nicht verlassen. Vielmehr wirkt die Grenzfläche wie ein sehr perfekter Spiegel und reflektiert den betreffenden Strahl gemäss dem Reflexionsgesetz. Wir sprechen von Totalreflexion.
Anwendung der Totalreflexion
Das Prinzip der Totalreflexion ermöglicht in der angewandten Optik eine ganze Anzahl interessanter Anwendungen. Für die einfache Umlenkung von Lichtstrahlen dienen sogenannte Umkehrprismen. Besteht das Prisma aus einem Medium, dessen Brechungsindex einen Grenzwinkel von weniger als 45° garantiert, wird an der Hypotenuse eines 90/45°-Prismas ein Lichtstrahl, der senkrecht auf eine Kathetenfläche auftritt, total reflektiert. Da der reflektierte Strahl wieder senkrecht auf die Grenzfläche der anderen Kathete auftrifft, kann er dort das dichtere Medium wieder verlassen. Im Gegensatz zu einem Spiegel braucht ein Umkehrprisma nicht versilbert zu werden. In einem Präzisionsgerät ist die Justierung dieser Umlenkeinheit präziser als beim Einsatz eines Spiegels.
Muss ein einfallender Lichtstrahl parallel zur Einfallsrichtung zurückreflektiert werden, schickt man den einfallenden Strahl am Rand der Hypotenusenfläche ins Prisma. Es wirkt dadurch doppelreflektierend. Das Prinzip des doppelreflektierenden Prismas ist im Prismenfeldstecher verwirklicht. Durch Anordnung zweier solcher Prismen lässt sich der Strahlengang gewissermassen «falten». Man erreicht eine kürzere Baulänge.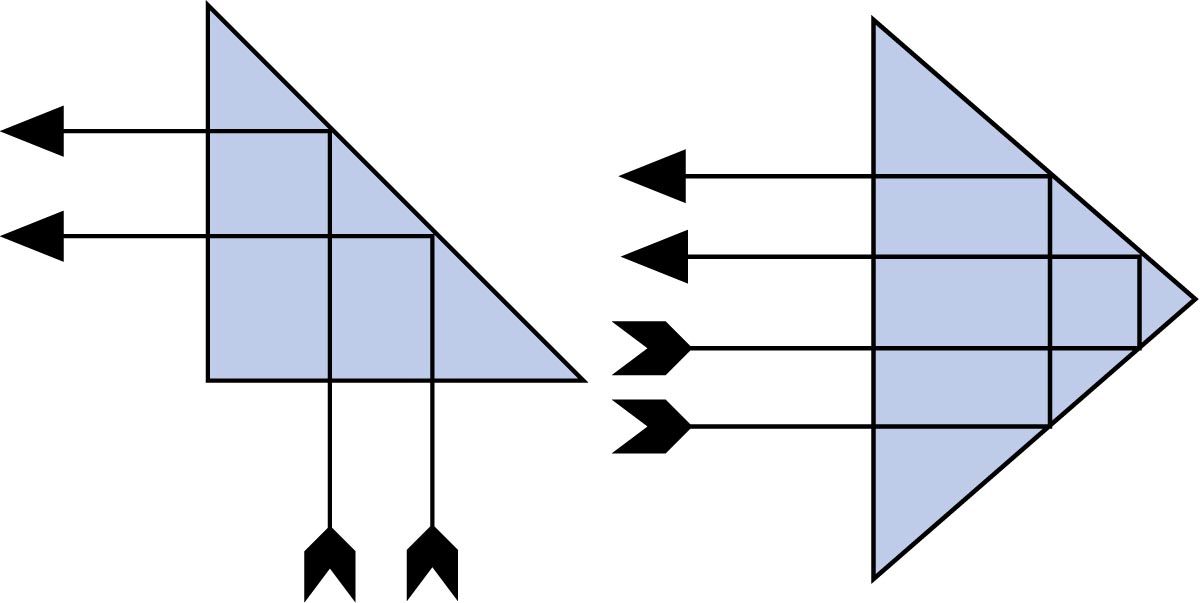
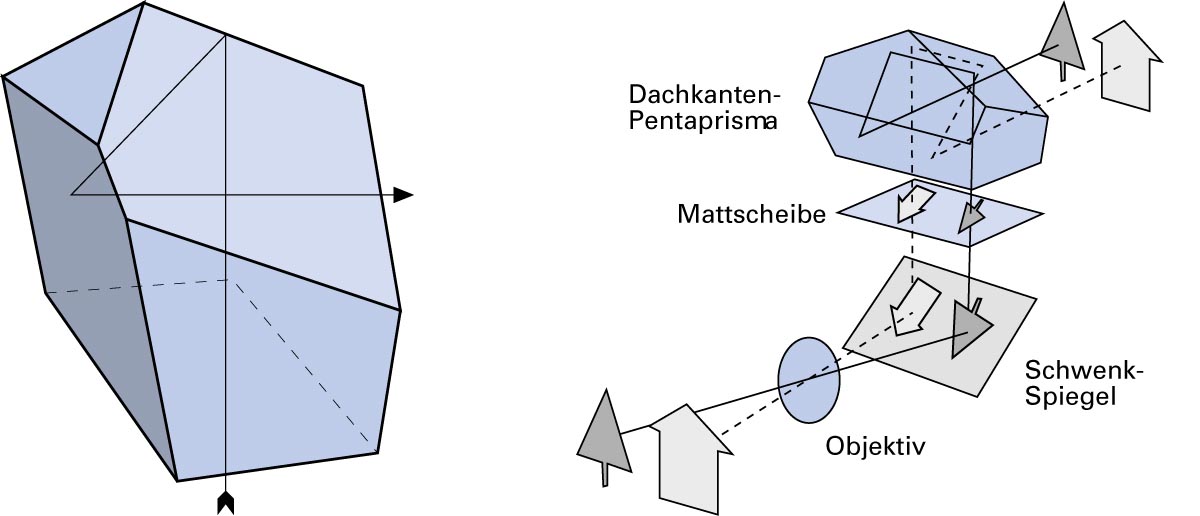
links: Umkehrprisma; rechts: Doppelreflektierendes Prisma
links: Dachkantenprisma; rechts: Einsatz des Dachkanten-Pentaprismas in der Spiegelreflexkamera
Ist eine totalreflektierende Fläche als Dachkante ausgeführt, wirkt diese wie ein Winkelspiegel und reflektiert das aufgefangene Bild seitenrichtig. Verwirklicht ist dieses Prinzip beim Dachkanten-Pentaprisma, wie es etwa in Kleinbild-Spiegelreflexkameras als Suchereinheit verwendet wird. Das Dachkanten-Pentaprisma hebt im Sucherokular die Seitenverkehrtheit des Mattscheibenbildes wieder auf.
Eine sehr interessante Anwendung stellt die Totalreflexion in einem Glasstab dar. Schickt man einen Lichtstrahl derart in einen Glasstab, dass er ausserhalb des Grenzwinkels auf die Aussenwandung trifft, kann er nicht austreten. Er wird vielmehr stetig total reflektiert.
Teilreflexion in einer Glasfaser
Bündelt man feine Glasfasern – von denen jede dieselben totalreflektierenden Eigenschaften besitzt – zu ganzen Paketen, entstehen Lichtleitfasern zur digitalen Nachrichtenübertragung oder bei einer grossen Anzahl dick gebündelter Fasern sogar eigentlich abbildende Faseroptiken (Endoskope). Flexible Lichtleiter, die auf diesem Prinzip beruhen, ermöglichen bei komplizierten Makroaufnahmen, das notwendige Aufnahmelicht gezielt zum Aufnahmeobjekt zu bringen. Es existieren im Handel dazu spezielle Leuchtgeräte mit verschieden langen beweglichen Lichtleitern. Auch Farbanalyzer, wie sie beim analogen Farbvergrössern zur Filterbestimmung gebraucht wurden, führen beispielsweise das Messlicht vom Vergrösserungsobjektiv mittels Lichtleitfasern zum Messgerät.
Teilreflexion
Sobald Licht auf eine Grenzfläche auftritt, kann jeweils nicht der gesamte Anteil in das andere Medium übertreten, denn ein geringer Teil des auffallenden Lichts wird gesetzmässig reflektiert. Der Lichtverlust ist abhängig vom Einfallswinkel, von der Differenz der Brechungsindizes beider Medien (dem Brechungsverhältnis) und natürlich auch von der Länge des Lichtweges in einem bestimmten Medium.
Weil diese Art der Reflexion nur einen bestimmten Anteil des Lichts betrifft, spricht man von Teilreflexion. Bei senkrechtem Lichteinfall lässt sich die Teilreflexion nach der Fresnelschen Reflexionsformel berechnen:
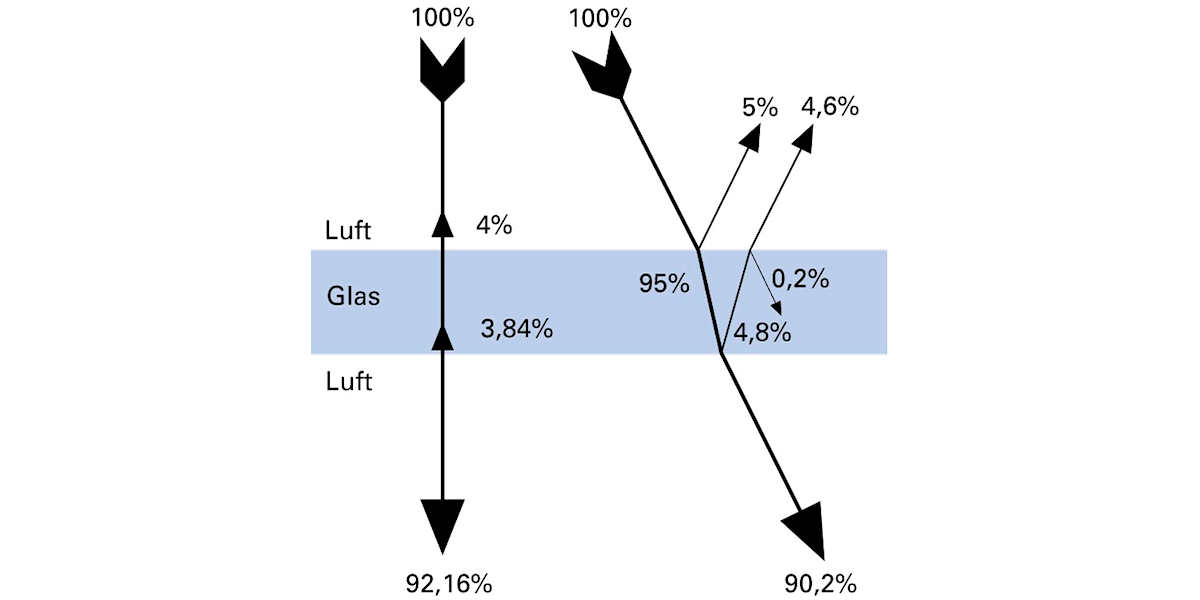
nA ist dabei der mittlere Brechungsindex des ersten brechenden Mediums, nB derjenige des zweiten brechenden Mediums. Für Glas mit dem Brechungsindex 1,5 beträgt demnach die Teilreflexion aus dem Medium Luft bei senkrechtem Lichteinfall 0,04 = 4%. Ist der Einfallswinkel grösser als 0°, so ist auch die Teilreflexion etwas grösser.
Teilreflexion tritt an jeder Grenzfläche auf. Beim Durchgang eines Lichtstrahls durch eine Glasplatte entstehen deshalb Verluste sowohl beim Eintritt wie auch beim Austritt des Strahls.
Teilreflexion bei Objektiven
Teilreflexion tritt natürlich auch dann auf, wenn Lichtstrahlen in den Glaskomplex eines Objektivs eintreten. Neben einem Lichtverlust treten hier noch andere Nachteile auf. Die Teilreflexion lässt Nebenbilder entstehen, die das eigentliche Bild überlagern. Bereits bei einer einfachen Linse resultiert ein Punktbild vor der eigentlichen Bildebene. Das Nebenbild ist zwar prozentual schwach, doch überlagert es unscharf den eigentlichen Bildpunkt und führt so zu einem Verlust an Bildbrillanz. Bei mehrlinsigen Objektiven wird der Effekt immer grösser.
links: Bei einem unvergüteten Triplet mit 6 Glas-Luft-Flächen und einer Glas-Glas-Fläche beträgt der Lichtverlust bereits 27%, das heisst gut eine halbe Blendenstufe!
rechts: Blendenflecken, hervorgerufen durch Teilreflexion an Glas-Luft- und Glas-Glas-Flächen im Objektiv.
Die Kumulation der gleichzeitig entstehenden Nebenbilder ist derart gross, dass vor allem im Spitzlichtbereich deutliche Fehlabbildungen zu bemerken sind. Der Effekt, der vorwiegend bei Gegenlichtaufnahmen zur Wirkung kommt, zeigt eine wenig trennscharfe Abbildung, mangelnde Bildbrillanz, Blenden-Phantomgebilde und Überstrahlungen.
Vergütung
Nach der Fresnelschen Reflexionsformel ist die Teilreflexion um so grösser, je höher das Brechungsverhältnis zweier Medien ist. Stellen wir uns vor, wir würden auf beiden Seiten einer Glasplatte, die durch Teilreflexion einen Transparenzverlust von etwa 8% aufweist, eine durchsichtige Schicht auftragen, deren Brechungsindex etwa in der Mitte zwischen demjenigen von Glas und demjenigen der Luft liegt. Es treten dadurch zwei Teilreflexionen auf, eine beim Eintritt in diese Schicht, die zweite bei der Grenzfläche Schicht-Glas. Wir brauchen lediglich beide Teilreflexionen auszurechnen, die Resultate zu addieren und erhalten so die gesamte Teilreflexion.
In unserem Berechnungsbeispiel soll der Brechungsindex dieser Schicht 1,22 betragen; derjenige von Glas 1,5:
Beim Austritt des Lichtstrahls aus der Glasplatte geschieht noch einmal dasselbe; der gesamte Teilreflexionsverlust beträgt demnach infolge dieser beiden Vergütungsschichten nur noch 4%
Trägt man statt lediglich einer solchen Vergütungsschicht deren mehrere mit abgestuften Brechungsindizes auf, verkleinert sich die Teilreflexion weiter. Vier übereinandergelegte Schichten mit den abgestuften Indizes 1,1; 1,2; 1,3 und 1,4 verkleinern die gesamte Teilreflexion in unserem Denkmodell auf 1,6%!
Einfluss der Interferenz
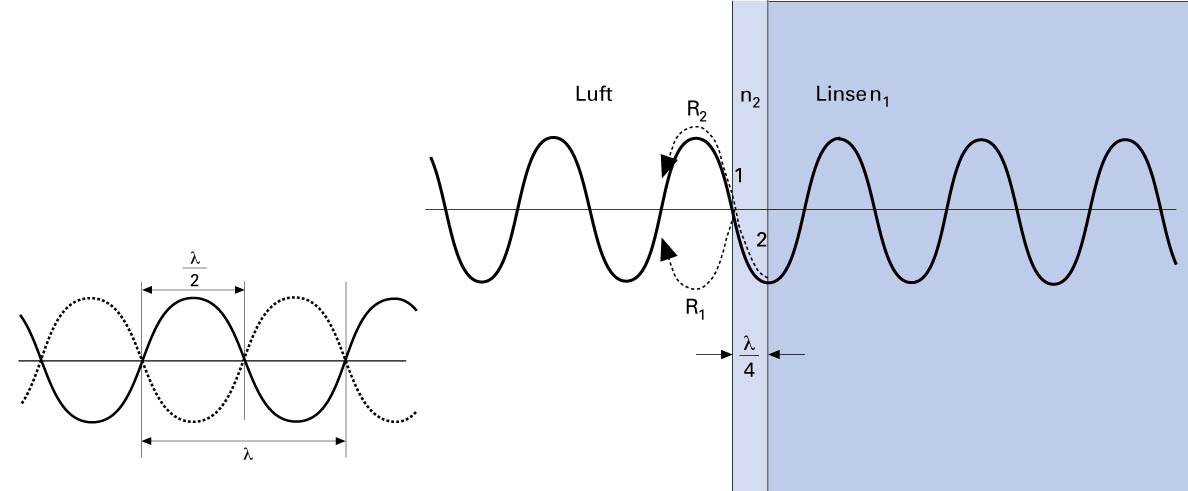
Bekanntlich lässt sich Licht durch Licht «eliminieren», sofern man zwei Wellen betrachtet, die von derselben Lichtquelle stammen. Gelingt es, einer Welle eine zweite mit gleicher Wellenlänge derart zu überlagern, dass sich von beiden Wellenzügen die Wellenberge mit den Wellentälern treffen, so wird die Energie gegenseitig aufgehoben. Dies ist dann der Fall, wenn die eine Welle gegenüber der anderen um eine halbe Wellenlänge verschoben ist.
links: Prinzip der Interferenz; rechts: Interferenz an einer Vergütungsschicht
Weist eine Vergütungsschicht eine Schichtdicke auf, die genau einem Viertel einer bestimmten Wellenlänge des sichtbaren Lichts entspricht und hat sie einen Brechungsindex, der aus der Wurzel der Brechzahl des folgenden Mediums errechnet wird, ist die Teilreflexion für diese Wellenlänge vollständig aufgehoben.
Stellt man die Vergütungsschicht in einer Dicke von etwa 125 nm her, so bewirkt diese bei der ersten und der zweiten Grenzschicht Teilreflexionen, die gegeneinander eine zeitliche Verschiebung von 250 nm aufweisen. Für Licht der Wellenlänge 500 nm ist dadurch eine gegenseitige Aufhebung gewährleistet. Licht dieser Wellenlänge wird dadurch nicht teilreflektiert.
Die Vergütung kann nur auf eine bestimmte Wellenlänge abgestimmt werden. Wird zum Beispiel die Vergütung auf 550 nm abgestimmt, so erscheint die Oberfläche dem Betrachter purpur, da ja rotes und blaues Licht immer noch reflektiert wird. Wird auf eine Wellenlänge von 450 nm abgestimmt, erscheint der Glaskörper dem Betrachter gelblich («Goldvergütung»).
Die Vergütungsschichten bestehen meist aus Leichtmetallfluoriden, die in einer Hochvakuumkammer auf die einzelnen Linsen aufgedampft werden. Bei einer sogenannten Mehrfachbeschichtung lassen sich die übereinandergelegten Einzelschichten mit unterschiedlichen Brechungsindizes zudem in unterschiedlichen Dicken herstellen. Dadurch ist die Teilreflexion für praktisch alle Wellenlängen nahezu komplett aufgehoben.
Objektive mit Mehrfachvergütung, sogenannte Multicoated-Objektive, weisen gegenüber einfachvergüteten oder gar unvergüteten eine bedeutend bessere Bildbrillanz und Farbsättigung auf. Phantombilder gehören damit der Vergangenheit an.
Wirkung der Vergütung bei einer extremen Gegenlichtaufnahme mit Objektiven aus unterschiedlichen Jahrzehnten.
links: Unvergütetes Objektiv Leitz Elmar 35 mm, 1936
Mitte: Einfachvergütetes Objektiv Auto Nikkor 35 mm, 1965
rechts: Mehrfachvergütetes Objektiv Zeiss Distagon 35 mm, 1990
Es ist kaum notwendig, die Glasoberfläche jeder Linse genau gleich mit vielen Einzelschichten zu belegen. Die Objektivhersteller tun dies nur dort, wo es auch wirklich notwendig ist. Sie haben zudem noch die Möglichkeit, durch Wahl der entsprechenden Leichtmetallverbindungen alle Objektive ihres Sortiments einander farblich anzugleichen, und erreichen damit, dass alle Objektivtypen, ob kurz- oder langbrennweitig, dieselbe Eigenfarbdichte besitzen.
Das Prinzip der Vergütung mit reflexionsmindernden Belägen (Antireflexbeläge) wurde in den Jahren 1934 bis 1936 von Bauer, Strong und Smakula in den Zeiss-Werken entwickelt, nachdem erste diesbezügliche Forschungen und Versuche bereits schon vorher bei Kern in Aarau gemacht wurden.
Hinweis: Bitte beachten Sie, dass die Vergütung lediglich die Teilreflexion reduziert oder beseitigt, aber keinerlei Einfluss auf den chromatischen Farbfehler (chromatische Aberration) hat, wie man gelegentlich fälschlicherweise hört oder liest. Zur Korrektur der chromatischen Aberration werden relativ kompliziert aufgebaute Objektive aus mindestens drei, meist aber einer grösseren Anzahl von Einzellinsen (4 bis 6) aus sehr verschiedenen Glassorten benötigt, welche gleiche Brennweiten für mindestens drei wichtige Wellenlängen erzeugen:
F‘ = 480,0 nm = Blaugrün
C ‚ = 643,9 nm = Rot
e = 546,1 nm = Gelbgrün
Üblicherweise bezeichnet man solche Objektivtypen als Apochromaten. Der chromatische Korrekturzustand ist dadurch über den gesamten Bereich der fotografisch aktinischen (belichtungswirksamen) Wellenlängen genügend gewährleistet, das heisst, im Bereich von 400 bis 700 nm treten nur sehr geringfügige Brennweitenunterschiede auf, die sich in der praktischen Fotografie nur wenig bemerkbar machen (siehe Folge 9).
Dispersion durch Refraktion
Ich habe bereits kurz angedeutet, dass die Grösse des Brechungsindexes auch von der Wellenlänge des Lichts abhängig ist. Mit der Brechzahl n meint man normalerweise den mittleren Brechungsindex nd, der Gültigkeit hat für die Spektrallinie d (Natrium-Linie), einer Wellenlänge von 587,6 nm. Daraus lässt sich bereits ableiten, dass die Grösse des Brechungsindexes für andere Wellenlängen im gleichen durchsichtigen Medium etwas anders ist.
Zerlegung des weissen Lichts
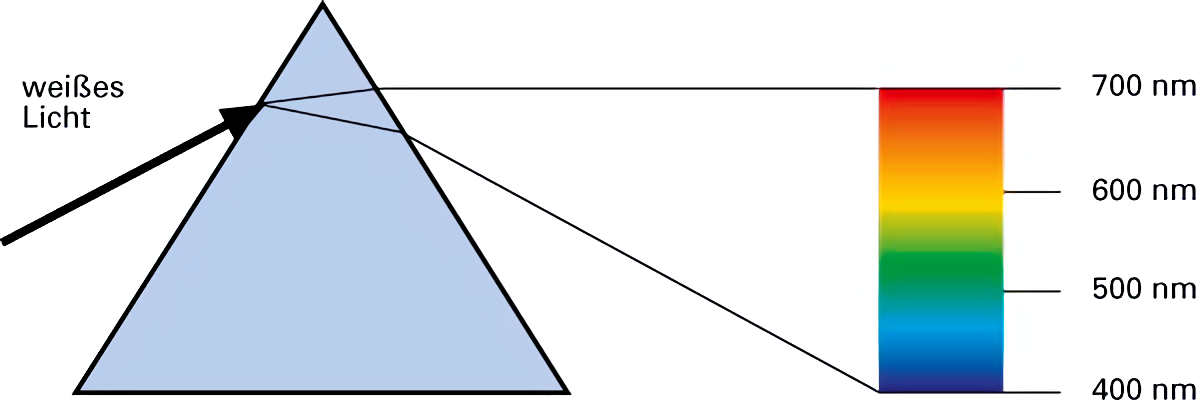
Andere Brechzahlen erzeugen eine abweichende Refraktionsstärke, das bedeutet, die Brechung beim Eintreten eines Lichtstrahls in ein optisch dichteres Medium muss auch von der Wellenlänge abhängig sein.Wir kennen das aus dem täglichen Leben; denken wir nur an einen Regenbogen! Tritt ein weisser Lichtstrahl nämlich in ein dichteres Medium ein, wird er nicht nur gebrochen, sondern auch gleichzeitig in einzelne Farben zerlegt.
Experimentell zeigt man das üblicherweise mit Hilfe eines Prismas. Fängt man den durch ein Prisma gebrochenen Lichtstrahl mit Hilfe eines Schirms oder einer Mattscheibe auf, erscheint auf dem Schirm ein farbiges Band. Man bezeichnet dieses Band als Spektrum und die einzelnen entstehenden Farben als Spektralfarben.
Chromatische Aberration
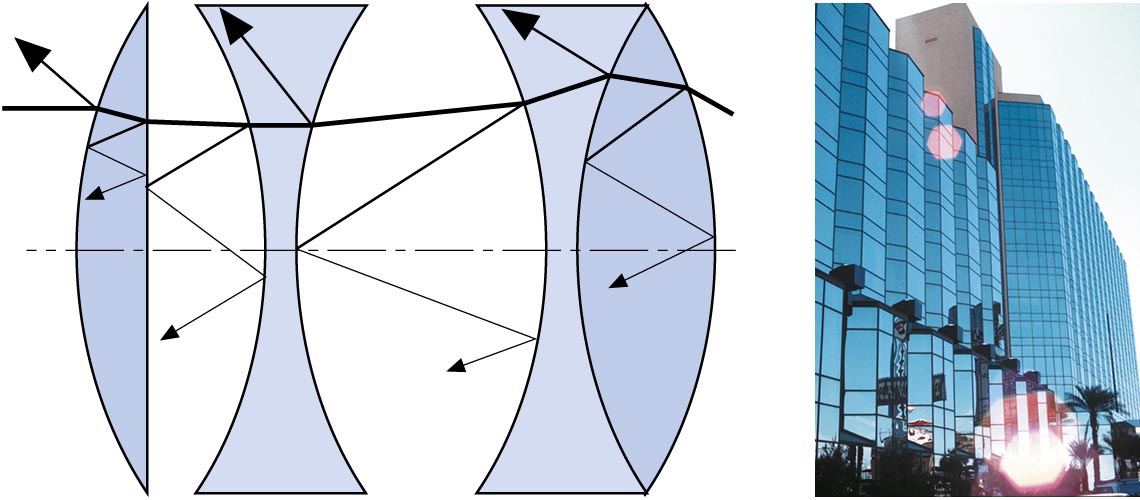
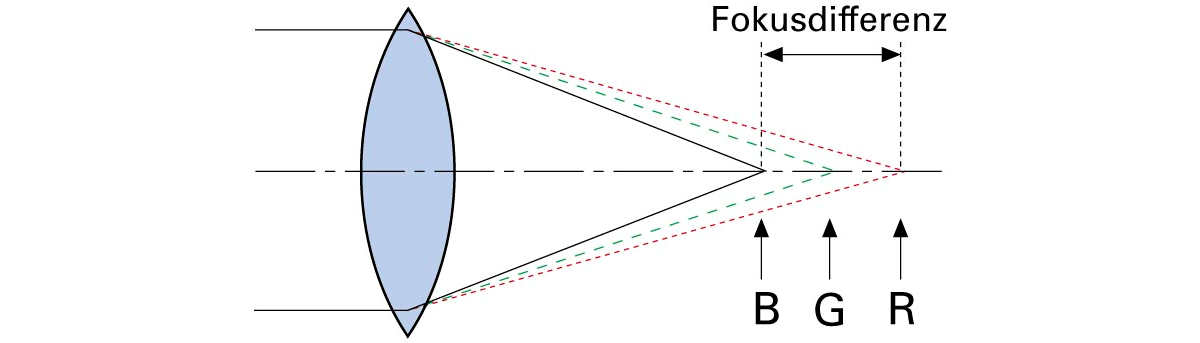
Bei der Brechung von Licht durch Linsen tritt ein gleicher Effekt ein, denn eine Linse lässt sich als Körper interpretieren, der aus lauter Prismen aufgebaut ist. Sendet man daher ein Parallelbündel weissen Lichts durch eine einfache Linse, entsteht nicht ein einzelner Brennpunkt. Vielmehr besitzt jede Farbe, das heisst sogar jede Wellenlänge der gebrochenen Strahlung, eine andere Bildweite, wie es die Abbildung unten für die additiven Grundfarben Blau, Grün und Rot zeigt. Je nach Glassorte liegt der Unterschied zwischen den Brennpunkten für blaue und rote Strahlung im Bereich von 2 bis 5% der Durchschnittsbrennweite. Die Differenz zwischen diesen Brennpunkten bezeichnet man als Fokusdifferenz; sie stellt den eigentlichen Farblängsfehler dar.
Chromatische Längsabberration
Moderne Objektive sind in aller Regel chromatisch gut korrigiert. Für normale Einsätze muss das Objektiv nur für das sichtbare Licht gleiche Brennweiten aufweisen. Da optisches Glas für Ultraviolett unter 390 nm nicht durchlässig ist, muss diese unsichtbare kurzwellige Strahlung nicht mit in die Korrektur einbezogen werden. Unter extremen Voraussetzungen wie im Hochgebirge über 3000 Meter über Meer bei strahlender Sonne empfiehlt es sich trotzdem, vor dem Objektiv einen UV-Sperrfilter einzusetzen, der bis etwa 410 nm sperrt. Den gleichen Zweck erfüllt ein (mehrfachvergüteter!) Skylight-Filter.
In Folge 9 werden wir uns noch intensiver mit den chromatischen Abbildungsfehlern auseinandersetzen.
© by Jost J. Marchesi
In der 4. Folge am nächsten Freitag geht es um Abbildungsverhältnisse und Perspektive.
Lesen Sie auch
Folge 1: «Licht, das «Rohmaterial» der Fotografie» (28.05.2021)
Folge 2: «Lichtausbreitung, Reflexion und Absorption» (04.06.2021)




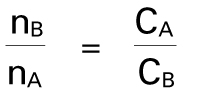

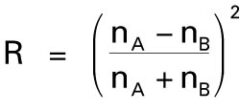
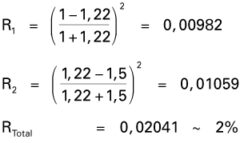

Geschwindigkeiten – von Fussgängern bis zur Lichtgeschwindigkeit – misst man als Wegstrecke, die pro Zeiteinheit zurück gelegt wird, also als Kilometer pro Stunde km/h, oder pro Sekunde km/s. Die im Text zu lesende Masseinheit „Sekundenkilometer“ (Sekunden, multipliziert mit Kilometern) hat deshalb keine Chance, die Optik zu revolutionieren oder Einstein zu widerlegen… Darauf wette ich zwei Sekundendeziliter Orangensaft!
Wenn im gleichen Abschnitt bereits zweimal der Ausdruck Kilometer pro Sekunde gebraucht wurde, schien es mir angebracht, ein drittes mal einen sprachlich etwas anderen Ausdruck zu verwenden, in der offensichtlich falschen Hoffnung, die meisten Leser würden verstehen, was ich damit meine. Zumal es zweifellos ein paar Menschen gibt, welche sogar den umgangssprachlich oft gehörten Ausdruck „Stundenkilometer“ richtig einordnen…
Einfach wunderbar, wieder einmal so tief in diese Materie eintauchen zu können, vielen Dank Jost J. Marchesi und FotoIntern!
Interessant: Licht wird beim Fotografieren mit einem maximalen Winkel γ = ca. 28°/k gebrochen, wobei k die Blendenzahl darstellt. Dies gilt für alle Strahlen, woher sie auch kommen und wo immer sie auf dem Sensor auftreffen (Faustregel). So mindert man die Aberrationen etwa um die Hälfte, wenn die Blendenzahl verdoppelt wird (Blende um 2 Stufen schließen). Beispiel: Mit Blende 4: γ = 7° (maximal); mit Blende 8: γ = 3.5° (maximaler Brechungswinkel des Lichts) …
Danke für die tolle Abhandlung!