Repetitorium OPTIK 4: Abbildungsverhältnisse und Perspektive

Starke stürzende Linien können den Eindruck von schwindelerregender Höhe verstärken. Aufnahme: Ilka Marchesi

Die einzige Aufgabe eines Objektivs ist die Verbesserung der Lichtstärke gegenüber der Lochkamera, das heisst, die Vergrösserung der Lichtdurchlassöffnung ohne dabei die Punktgrösse eines winzig kleinen Gegenstandpunktes erkennbar zu verändern. Trotz ihrer unglaublichen Banalität ist diese Aussage die einzig wesentliche Definition. Im Gegensatz zur Camera Obscura, bei welcher aktueller Kamerauszug und Brennweite identisch sind, muss beim Einsatz eines Objektivs zwischen diesen Kardinalswerten des Abbildungsmassstabs unterschieden werden.

 

Funktion des Objektivs

Um unsere Überlegungen zur eigentlichen Funktion eines Objektivs zu vervollständigen, sollten Sie das Abbildungsprinzip der Lochkamera (in Folge 2) studieren. Für eine einigermassen erkennbare Abbildungs­-Schärfe muss die Belichtungsöffnung bei einer Lochkamera klein sein, was einer sehr geringen Lichtstärke entspricht. Unsere Beispiel-Lochkamera aus Folge 2 hatte eine Lichtstärke von lediglich 1:300 (entsprechend Blende 300). Um die Lichtstärke zu verbessern, muss daher der Durchmesser der Belichtungsöffnung vergrössert werden.

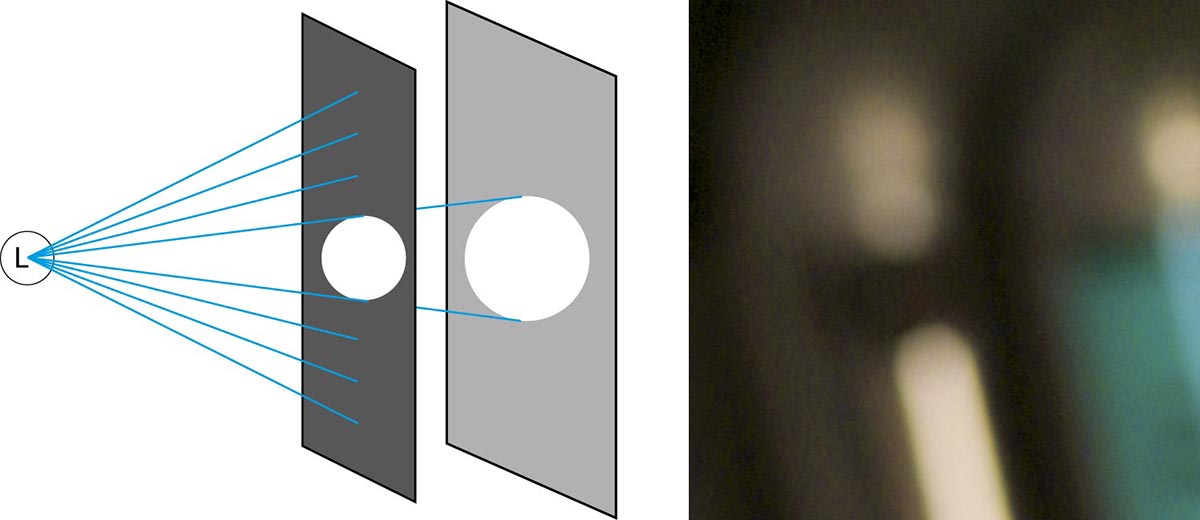
Würde nun mit einer solchen lichtstärkeren Camera Obscura fotografiert, entstünden als kleinste Bildpunkte flächige Scheiben, die sich gegenseitig zum Bild überlagern. Das Bild würde aus vielen solchen kreisförmigen «Unschärfekreisen» bestehen, die sich gegenseitig überlagern. Das Bild sähe dann völlig unscharf aus.

 

Durch Vergrössern der Belichtungsöffnung bei einer Lochkamera entsteht ein unscharfes Bild.

Um trotz vergrösserter Belichtungsöffnung einen scharfen Abbildungspunkt zu erhalten, müssten sich die Lichstrahlen beim Passieren der Belichtungsöffnung wieder auf einen Punkt konvertieren lassen.

 

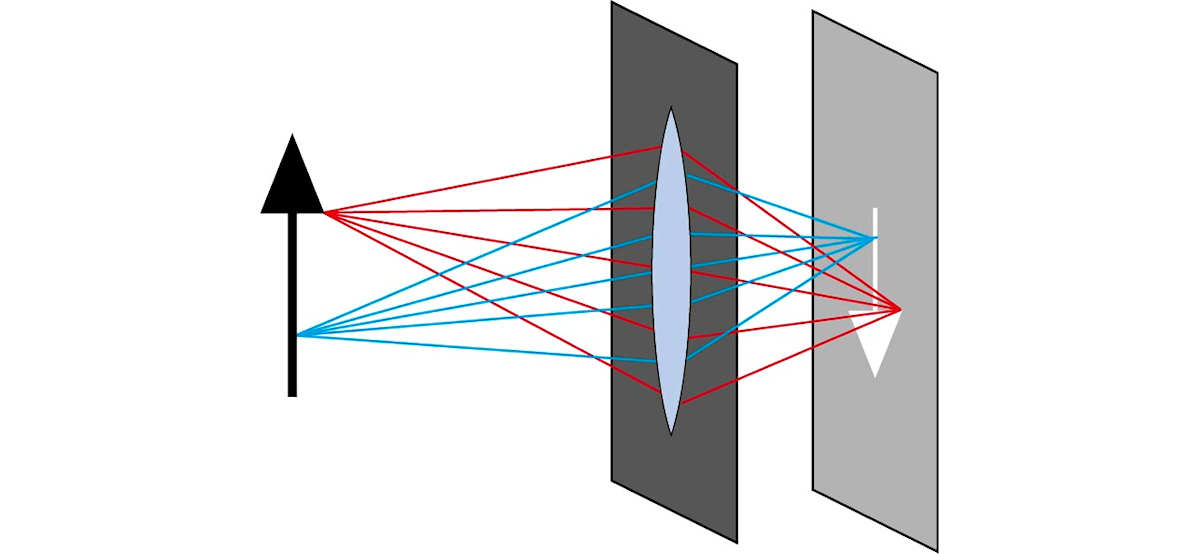
Durch ein sammelndes System als Belichtungsöffnung entsteht trotz grossem Durchmesser eine punktförmige Abbildung divergenter Strahlenbündel.

 Dazu wird ein brechendes Medium zum Beispiel aus Glas in Form einer Linse benötigt. Tritt ein Lichtstrahl schräg in ein optisch dichteres Medium ein, wird es von seiner geradlinigen Ausbreitung abgelenkt, weil sich die Lichtausbreitungs-Geschwindigkeit entsprechend der optischen Dichte des Mediums verringert (Brechung des Lichts, siehe Folge 3).

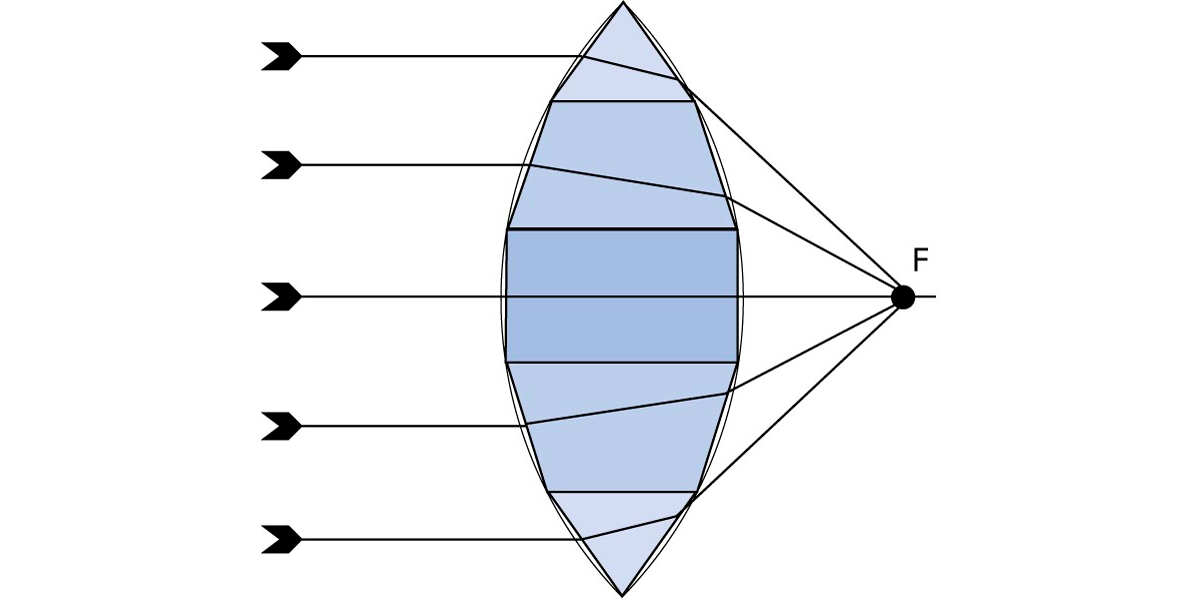
Stellt man sich einen Glaskörper vor, der aus mehreren übereinander gelegten Glasprismen besteht, kann dies als Linsenform interpretiert werden. Ein auf dieses Gebilde fallendes Parallelbündel wird durch die unterschiedlichen Prismenwinkel der Einzelprismen entsprechend unterschiedlich gebrochen. Jeder einzelne Strahl verhält sich gesetzmässig. Sind die Formen der Einzelprismen aufeinander abgestimmt, treffen sich alle Strahlen eines Parallelbündels in einem Punkt, dem Brennpunkt F’.

 

Brechung an Linsen. Brechung eines Parallelbündels an einer Konvexlinse, welche als Summe aufeinander abgestimmter Glasprismen interpretierbar ist.

Hinweis: Stellen wir uns einen winzig kleinen Gegenstandspunkt vor, auf den Licht fällt. Dieser Punkt reflektiert das Licht allseitig divergent (von einem Punkt auseinanderlaufend). Mit zunehmender Ausbreitungsdistanz erscheint das Bündel immer paralleler, bis es schliesslich in unendlicher Distanz als paralleles Strahlenbündel angesehen werden kann. In unseren schematischen Darstellungen sind daher parallele Strahlen immer das Synonym derjenigen Strahlen, die von einem einzelnen Gegenstandspunkt in unendlicher Entfernung stammen. Üblicherweise gilt es in der Fotografie, diese wieder zum möglichst kleinen Bildpunkt zu vereinen (konvergieren). Strahlen von einem Gegenstandspunkt näher als Unendlich fallen demgegenüber auseinander laufend (divergent) auf das Linsensystem.

Stellen wir uns weiter vor, wir würden die geraden Flächen der Prismen anschleifen, bis ein kontinuierlicher Übergang geschaffen ist, so entsteht ein neues, jeden Strahl entsprechend kontinuierlich brechendes Gebilde, eine Sammellinse. Eine Sammellinse, auch als Konvexlinse bezeichnet, kann man sich aus unendlich vielen Einzelprismen aufgebaut vorstellen. Wie aus der Darstellung oben ersichtlich, hat eine solche Konvexlinse abbildende Eigenschaften. Das auf die Linse fallende Parallelbündel ist ja nichts anderes als die Fortsetzung des divergenten (auseinander laufenden) Bündels eines sich im Unendlichen befindenden Gegenstandspunkts. Die Linse bildet im Punkt F’, dem Brennpunkt, diesen unendlich weit entfernten Gegenstandspunkt als scharfen Bildpunkt ab.

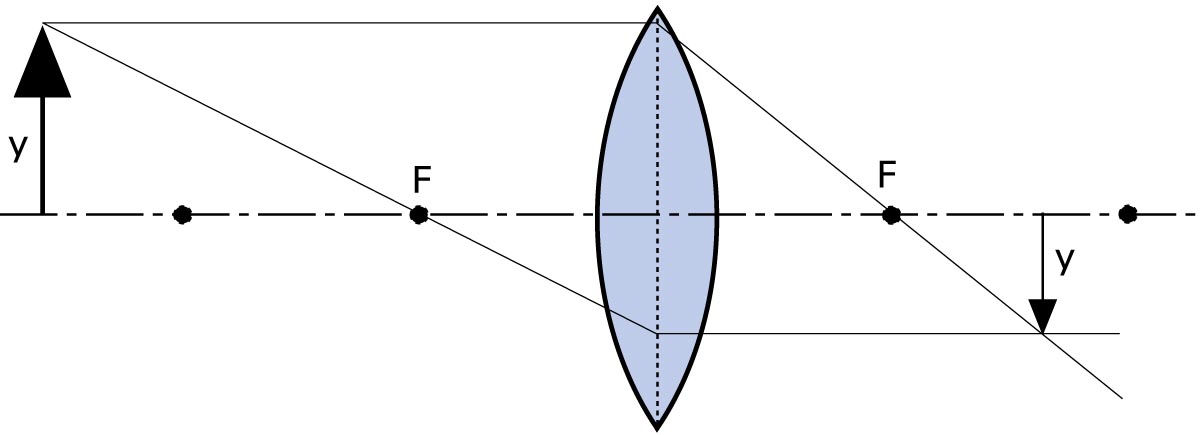
Ähnliches geschieht, wenn wir einen Gegenstandspunkt betrachten, der sich näher bei der Linse befindet. Das von diesem Gegenstandspunkt ausgehende divergente Strahlenbündel wird von der Linse ebenfalls in einem Punkt (Bildpunkt P’) gesammelt, der sich jedoch weiter von der Linse entfernt befindet als derjenige, der sich aus einem Parallelbündel gebildet hat.

Je nach Entfernung eines Gegenstandes von der Linse (Aufnahmedistanz a) entsteht das Bild auf dem Brennpunkt (Aufnahmedistanz unendlich) oder weiter vom Brennpunkt entfernt.

Oder anders gesagt: Die Bildentfernung a’ (Distanz zwischen Linse und Bild) ist abhängig von der Aufnahmedistanz. Die Grösse des entstehenden Bildes im Verhältnis zur Gegenstandsgrösse (Abbildungsmassstab) ist von Aufnahmedistanz und Brennweite abhängig.

 

Bewegungsregel

Befindet sich der Gegenstand unendlich weit entfernt, steht das Bild genau auf einfacher Brennweite im Bildraum.

Die folgenden drei Abbildungen zeigen die typischen Abbildungsorte, wenn sich der Gegenstand von Unendlich in Richtung Objektiv bewegt.

 

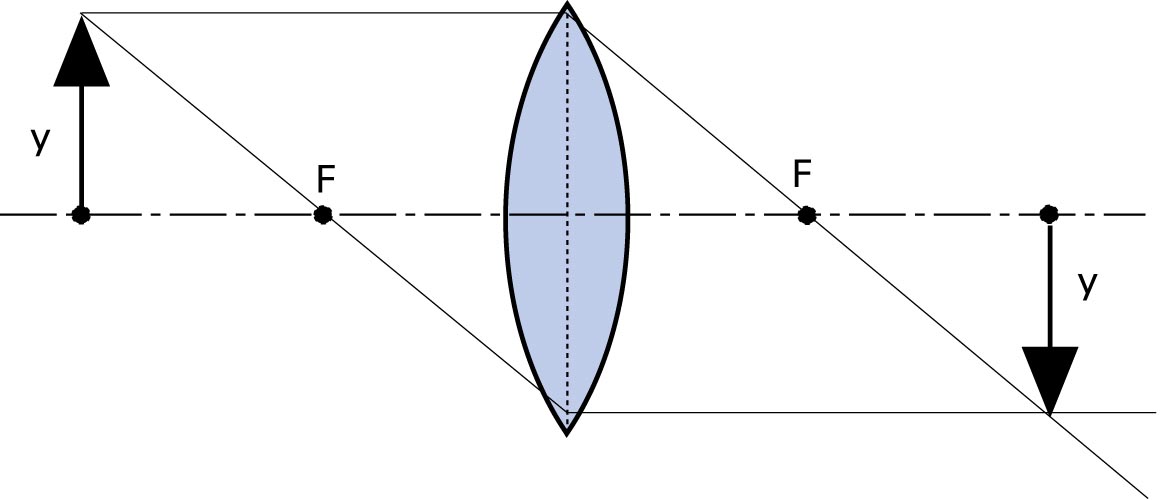
Gegenstand ausserhalb doppelter Brennweite

Befindet sich der Gegenstand in einem Raum zwischen und etwas ausserhalb der doppelten Brennweite vor dem Objektiv, entsteht das Bild hinter dem Objektiv in einer Ebene, die zwischen einfacher und doppelter Brennweite liegt. Dies entspricht den meisten Aufnahmesituationen.

 

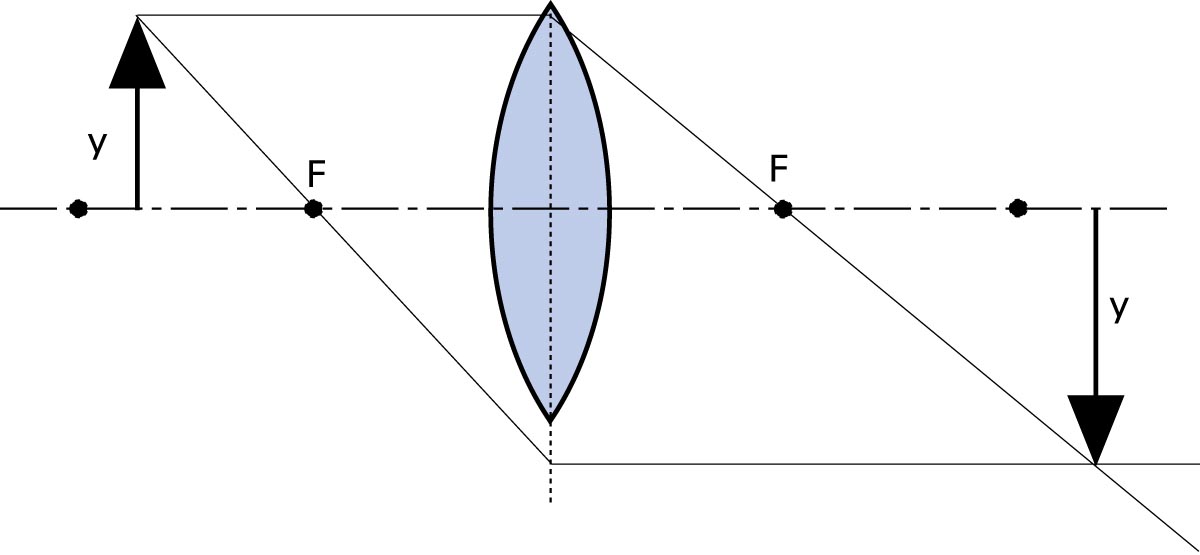
Gegenstand genau auf einfacher Brennweite

Befindet sich der Gegenstand genau auf doppelter Brennweite im Gegenstandsraum, liegt das Bild in einer Bildebene, die sich ebenfalls in doppelter Brennweitenentfernung im Bildraum befindet. Aufnahmedistanz und Kamera-Auszug sind gleich gross, beide doppelt so lang wie die Brennweite. Das Bild ist gleich gross wie der Gegenstand; der Abbildungsmassstab beträgt 1:1.

 

Gegenstand zwischen einfacher und doppelter Brennweite

Wandert der Gegenstand noch näher zum Objektiv und befindet er sich im Gegenstandsraum zwischen doppelter und einfacher Brennweite, liegt das Bild im Bildraum ausserhalb der doppelten Brennweite und ist grösser als der Originalgegenstand. Läge der Gegenstand genau auf einfacher Brennweite, entstünde im Bildraum ein Bild, das unendlich gross wäre und unendlich weit entfernt abgebildet würde (Umkehrung des ersten Falls, bei dem sich der Gegenstand unendlich weit entfernt befand). Die Aufnahmedistanz muss daher immer grösser sein als die Brennweite des Objektivs, sonst entsteht kein reelles Bild mehr.

 

    

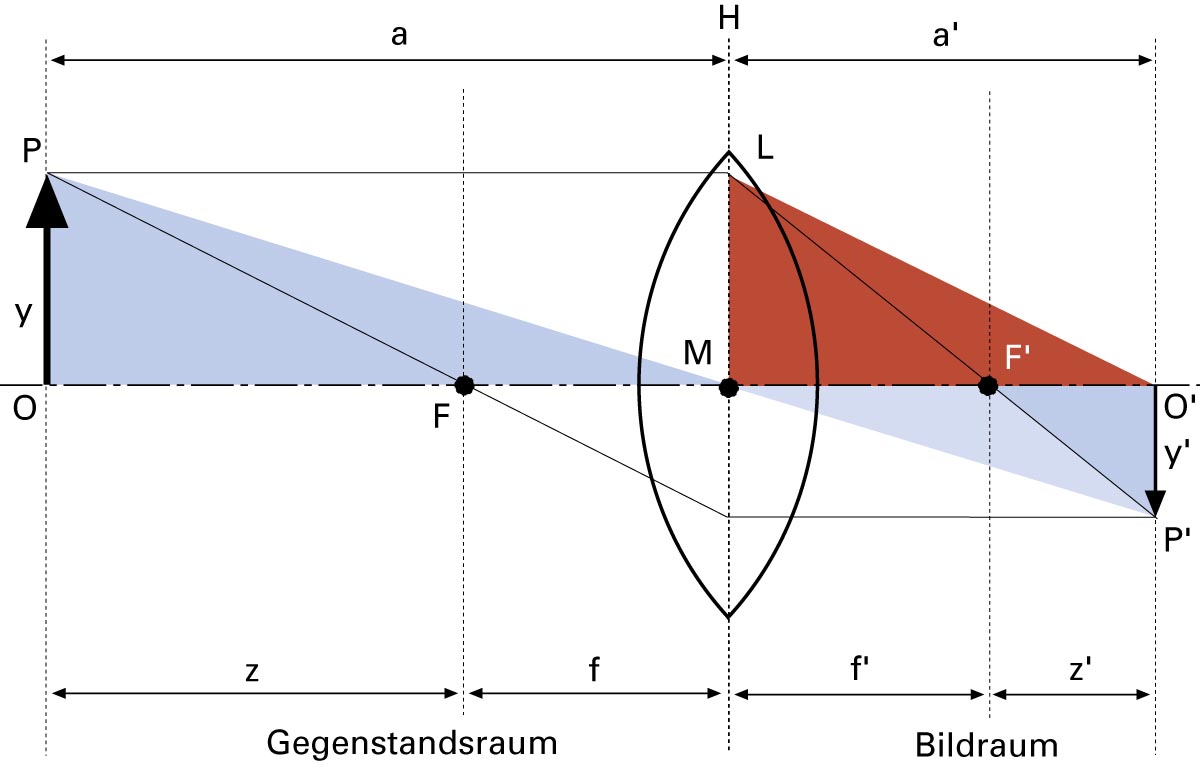
Terminologie

L       =       Linse
M      =       Mittelpunkt
H       =       «Hauptebene», in der die Hauptpunkte liegen. Vereinfacht 
                    dargestellt. Für präzise Brennweiten-Berechnungen sind
                    die Hauptpunkte H und H‘ notwendig.
F       =       gegenstandseitiger Brennpunkt, Dingbrennpunkt
F‘      =       bildseitiger Brennpunkt, Bildbrennpunkt
f        =       gegenstandseitige Brennweite *, dingseitige Brennweite
f‘        =       bildseitige Brennweite *
a       =       Gegenstandsentfernung, Dingweite, «Aufnahmedistanz»
a‘      =       Bildentfernung, Bildweite, «Kameraauszug»
z        =       brennpunktbezogene Gegenstandsentfernung (a–f)
z‘       =       brennpunktbezogene Bildentfernung (a’–f
y       =       Strecke in der Gegenstandsebene, meist Gegenstandsgrösse
y‘       =       Strecke in der Bildebene, meist Bildgrösse
P       =       Gegenstandspunkt, Dingpunkt 
P‘      =       Bildpunkt
O      =       Gegenstandspunkt auf der Achse, Dingpunkt auf der Achse
O‘      =       Bildpunkt auf der Achse         

                    * im Medium Luft ist f und f‘ gleich gross

 

Aufgabe des Objektivs

Wir sehen also, dass wir mit Hilfe eines zusätzlichen optischen Mittels, einer sammelnden Linse, die Forderung erfüllen können, trotz vergrösserter Belichtungsöffnung eine punktförmige Abbildung zu erreichen. Der einzige Nachteil gegenüber der Belichtungsöffnung durch ein kleines Loch: Das Bild erscheint nur noch in einer korrekt eingestellten Bildentfernung scharf. Bei der Lochkamera mussten wir darauf keine Rücksicht nehmen. Wählten wir einen langen Kameraauszug, entstand ein enger Bildausschnitt, bei kurzem Kameraauszug dagegen ein entsprechend weitwinkligeres Bild. Wird die Lochkamera durch den Einsatz einer Linse in ihrer Lichtstärke verbessert, geht dieser Komfort verloren; es gibt nur noch einen einzigen korrekten Kameraauszug, der von der Brennweite der Linse und von der Aufnahmedistanz abhängig ist.

Eine einzelne Linse ist mit vielen Abbildungsfehlern behaftet, auf die wir in einer späteren Lektion eingehen werden. Man korrigiert dies durch das Zusammenfügen mehrerer unterschiedlicher Linsen aus verschiedenen Glassorten zu einem Objektiv.  Die Aufgabe des Objektivs bleibt jedoch dieselbe. Man kann es nicht oft genug wiederholen: Die einzige Aufgabe des Objektivs ist die Erhöhung der Lichtstärke, das heisst, die Vergrösserung der Lichtdurchlassöffnung.

 

Brennweite

Eine der Kardinalsgrössen bei den Objektivdaten ist die Brennweite. Je nach Brechkraft der Linsen hat ein Objektiv eine kürzere oder längere Brennweite und benötigt daher in der Kamera einen kürzeren oder längeren Auszug.

Um den Begriff der Brennweite zu klären, erinnern wir uns an Brennweiten­Bestimmungen, die wir als Kinder gemacht haben. Sicher waren auch Sie Besitzer eines «Brennglases» oder einer Briefmarkenlupe, was nichts anderes als eine einfache Sammellinse war. Damit haben wir die parallel einfallenden Strahlen der Sonne durch Abstandsänderung auf einen Punkt gebündelt und mit dem entstandenen Brennpunkt ein Papier oder ein Stück Holz anzubrennen versucht. Betrachten Sie dazu noch einmal die Abbildung «Brechung an Linsen», die das Brechungsprinzip der Sammellinse zeigt. Dort sind links der Linse parallel einfallende Lichtstrahlen gezeigt. Parallele Strahlen symbolisieren das Strahlenbündel, das von einem Gegenstandspunkt herkommt, der sich in unendlicher Entfernung befindet. Durch die brechenden Eigenschaften der Linse werden diese parallel einfallenden Strahlen zu einem einzigen Punkt gesammelt, dem Brennpunkt, der zudem das Bild des unendlich weit entfernten Gegenstands darstellt. Als Brennweite wird die Distanz zwischen der Linse und diesem Brennpunkt bezeichnet.

Die Brennweite ist abhängig von der Glasart, die zur Linsenherstellung verwendet wurde sowie von deren Krümmung und Dicke. Je nach seiner Brennweite erzeugt ein Objektiv die bilderzeugenden einzelnen Konvergenzpunkte in kleinerer oder grösserer Entfernung und lässt dadurch unterschiedlich grosse Bilder entstehen. Da wir jedoch normalerweise mit unserer Kamera immer das gleich grosse Negativformat verwenden, entsteht auf dem gleichbleibenden Negativformat ein mehr oder weniger grosser Ausschnitt der Gegenstandsebene.

 

Brennweite und Gegenstandsgrösse: Bei gleicher Aufnahmedistanz wird das Bild bei längerer Brennweite grösser.

 

Abbildungsmassstab und Perspektive

Mit Hilfe unseres doppeläugigen Sehens erkennen wir die Tiefe eines dreidimensionalen Raums, wir sehen räumlich. Schliessen wir hingegen ein Auge, haben wir bekanntlich recht grosse Mühe, diese dritte Dimension, die Tiefe des Raums, genau abzuschätzen. Sie kennen das unsichere Gefühl beim Autofahren, wenn Ihnen aus irgendeinem Grund ein Auge tränt und Sie gezwungen sind, ein kleines Stück einäugig zu fahren. Wir sind in solchen Fällen weitgehend unfähig, Distanzen richtig abzuschätzen.

Bei den üblichen Abbildungsverfahren entfällt – mit Ausnahme der Stereofotografie – das doppeläugige Sehen. Normale Kameras haben ein einziges Objektiv, die Darstellung entspricht der einäugigen Betrachtung. Dadurch werden die drei Dimensionen eines Gegenstandes auf deren zwei reduziert, nämlich auf Höhe und Seite des flächigen Bildes. Die dritte Dimension muss mit Hilfe der Perspektive vorgetäuscht werden. Das geschieht in der Fotografie, die nach den Gesetzen der Zentralperspektive arbeitet, automatisch. Wir haben jedoch verschiedene Möglichkeiten, diese natürliche Tiefenprojektion zu beeinflussen.

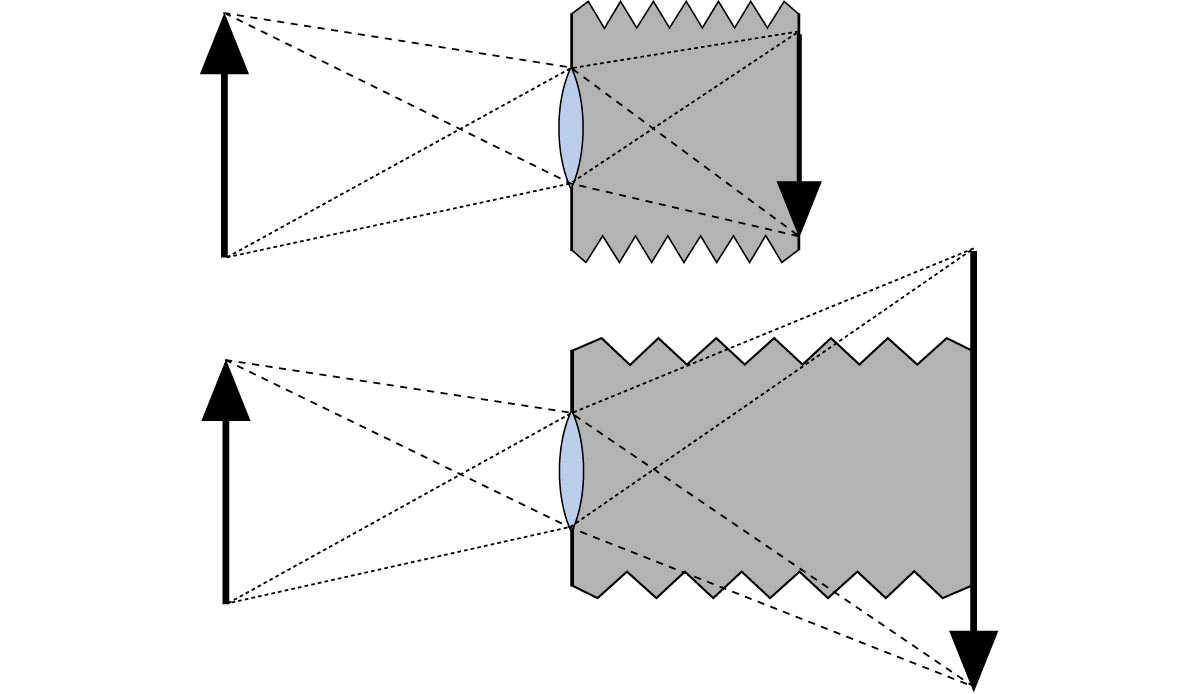
Der Abbildungsmassstab, das heisst, das Verhältnis der Bildgrösse (Abbildungsgrösse in der Filmebene) zur Gegenstandsgrösse wird bei gleicher Aufnahmedistanz mit zunehmender Brennweite immer grösser. Sonst ändert sich aber nichts! Vergrössert man nämlich eine Aufnahme – die mit kürzerer Brennweite gemacht wurde – so weit, bis das abgebildete Objekt dieselbe Grösse aufweist wie auf dem Bild, das mit langer Brennweite aufgenommen wurde, sieht man zwar eine geringere Bildschärfe jedoch keinen Unterschied in perspektivischer Hinsicht. Die Objektivbrennweite allein hat demnach keinen Einfluss auf die Perspektive. Bezeichnungen wie «Tele- oder Weitwinkelperspektive», die eine Abhängigkeit der Perspektive zur Objektivbrennweite suggerieren, sind daher reine Hirngespinste.

Sie können sich dieses zwar selbstverständliche aber immer wieder falsch erläuterte Grundgesetz auf einfache Weise vergegenwärtigen. Meine Studenten müssen sich dazu die «Goldene Kamera» – wie ich sie nenne – bauen. Es handelt sich dabei lediglich um eine Ausschnittmaske, ein Stück schwarze Pappe mit einem rechteckigen Ausschnitt im Seitenverhältnis 2:3 (dem Kleinbildformat entsprechend).

Kneifen Sie nun ein Auge zu und betrachten Sie die Umwelt durch diese Maske. Halten Sie das Hilfsmittel nahe ans Auge. Der gesehene Ausschnitt entspricht einer Kamera mit kurzer Brennweite (und zwar einer Brennweite, die gleich gross ist wie die Distanz zwischen Auge und Ausschnittmaske). Vergrössern Sie nun sukzessive die Distanz zwischen Maske und Auge und Sie sehen den Bildaussschnitt mit der entsprechend längeren Brennweite. Fixieren Sie einen einfachen kubischen Gegenstand durch die Maske und studieren Sie den Verlauf der Fluchtlinien (dritte Dimension). Wenn Sie nun die Brennweite verändern, indem Sie den Abstand zwischen Maske und Auge variieren, stellen Sie fest, dass sich am Verlauf der Fluchtlinien absolut nichts ändert. Sie haben damit einen handfesten Beweis, dass sich durch Ändern der Brennweite absolut nichts an der Perspektive verändert.

 

Bei gleichbleibender Aufnahmedistanz ändert sich an der Perspektive nichts, unabhängig der verwendeten Objektivbrennweite. Die Bilder demonstriert den Versuch mit der Ausschnittmaske (verschiedene Brennweiten, gleicher Standort).

 

Diese beiden Bilder sind bei gleichem Aufnahmeabstand (Kamera auf Stativ fixiert) entstanden; links mit der Normalbrennweite 50 mm rechts mit der Brennweiteneinstellung 200 mm. Und selbstverständlich entstehen dadurch keinerlei perspektivische Änderungen; lediglich der Bildausschnitt wird entsprechend enger!

Im nächsten Versuch sollten Sie eine festbleibende Brennweite simulieren (gleichbleibender Abstand zwischen Ausschnittmaske und Auge). Betrachten Sie damit am besten wieder einen kubischen Gegenstand aus grösserer Distanz. Gehen Sie nun langsam näher an den Gegenstand heran und beobachten Sie, wie sich die Fluchtlinien in Bezug auf die Kanten der Ausschnittmaske verändern. Sie werden feststellen, dass die Fluchtlinien bei grossem Betrachtungsabstand erheblich paralleler aussehen als bei geringem Abstand. Die Perspektive ändert sich zwar nicht beim Verändern der Brennweite, dagegen ist sie von der Aufnahmedistanz direkt abhängig. Je kürzer die Aufnahmedistanz ist, um so extremer wird das Verhältnis zwischen gleichen Strecken im Bildvordergrund und im Bildhintergrund. Bei grosser Betrachtungsdistanz scheint die Hinterkante des zu betrachtenden Kubus ähnlich lang wie die Vorderkante; die Fluchtlinien verlaufen nur sehr gering aufeinander zu. Bei kleiner Betrachtungsdistanz dagegen ist das Längenverhältnis der Vorderkante zur nunmehr deutlich kürzeren Hinterkante extrem; die Fluchtlinien verlaufen stark konvergent und treffen sich irgendwo im weiteren Hintergrund zum sogenannten Fluchtpunkt.

 

links: Kurze Aufnahmedistanzen ergeben stark divergierende Fluchtlinien.
rechts: Grosse Aufnahmedistanzen ergeben weniger stark divergierende Fluchtlinien.

Wenn ich eine Brennweitenvergrösserung vornehme, wird lediglich der Bildausschnitt enger, an der Konvergenz der Fluchtlinien ändert sich nichts. Versuche ich dagegen, denselben Bildausschnitt mit gleichbleibender Brennweite zu erzeugen, muss ich näher an den Gegenstand heran, wodurch die Fluchtlinien stärker konvergent verlaufen. Das obige Beispiel mit dem Getränkekasten verdeutlicht diese Begebenheit. Die linke Aufnahme entstand aus sehr geringer Aufnahmedistanz. Um den Gegenstand formatfüllend darzustellen, war ein Aufnahmeobjektiv mit kurzer Brennweite notwendig. Die rechte Aufnahme entstand dagegen in gleicher Aufnahmerichtung, aber aus einer erheblich grösseren Entfernung. Um den Gegenstand ebenfalls formatfüllend abzubilden, war ein Objektiv mit entsprechend längerer Brennweite notwendig.

Wir können es auch anders formulieren: Das kurzbrennweitige Objektiv ergibt eine kurze Aufnahmedistanz, wenn der zu fotografierende Gegenstand formatfüllend aufgenommen werden soll. Der Unterschied der Aufnahmedistanz zwischen den nächstliegenden und dem entferntesten Gegenstandspunkt ist beträchtlich; der Grössenunterschied gleicher Gegenstandsstrecken (zum Beispiel die hintere Horizontalkante) ist es daher ebenfalls. Bei der zweiten Aufnahme mit der längeren Objektivbrennweite wird zur formatfüllenden Aufnahme eine erheblich grössere Aufnahmedistanz verlangt; der Unterschied der Aufnahmedistanz zwischen nächstem und entferntestem Objektpunkt ist fast bedeutungslos geworden.

Wir können folgern: Eine kurze Aufnahmedistanz lässt stärker divergierende Fluchtlinien entstehen als eine grosse Aufnahmedistanz. Dass wir zur formatfüllenden Aufnahme im ersten Fall eine kürzere Brennweite benötigt haben, ist rein sekundär und hat auf den Fluchtlinienverlauf keinen Einfluss.

Da der Abbildungsmassstab m das Verhältnis zwischen dem um die Brennweite reduzierten Kameraauszug (a’–f = z’) zur Brennweite ist, können wir folgern: Die Perspektive ist allein und einzig vom Abbildungsmassstab abhängig. Ändere ich lediglich f, so wird automatisch auch a’ und damit z’ geändert; am Abbildungsmassstab (und somit an der Perspektive) ändert sich nichts.

 

Zentralperspektive

Die Fotografie arbeitet nach den Regeln der Zentralperspektive. Im Wesentlichen lassen sich diese wie folgt umschreiben:

• Ein Gegenstand wird um so kleiner abgebildet, je weiter weg er sich befindet.
• Von zwei gleich grossen Gegenständen wird der weiter entfernte kleiner
• Senkrechte Linien bleiben senkrecht, gleichgültig ob sie sich nah oder fern befinden.
• Waagrecht verlaufende Linien behalten ihre Richtung bei.
• In die Tiefe des Raums führende Linien laufen auf die auf der Horizontlinie liegenden Fluchtpunkte zu
• Die Perspektive wird durch den Standort und damit durch die Aufnahmedistanz bestimmt, nicht durch die Brennweite. Um eine bestimmte Wunschperspektive darzustellen, wählt man zuerst die benötigte Aufnahmedistanz. Die Wahl der Brennweite ist sekundär und dient lediglich zur Bestimmung des gewünschten Bildausschnitts!

 

Proportionen

Aus unseren Überlegungen haben wir erkannt, dass die Wahl der Perspektive durch den Aufnahmestandpunkt auch zwangsläufig einen Einfluss auf die Proportionen haben muss. Um sich darüber klar zu werden, sollten Sie zwei gleich grosse Gegenstände – zum Beispiel Ihre Schuhe – in einer Entfernung von rund 50 cm voneinander auf den Tisch legen und das Arrangement durch die Ausschnittmaske betrachten. Was stellen Sie fest? Durch unterschiedliche Betrachtungsabstände verändert sich erstens die Divergenz der Fluchtlinien und damit die Form der Gegenstände; gleichzeitig ändern sich aber auch die Grössenverhältnisse der beiden Gegenstände zueinander. Der Grund ist klar ersichtlich: Ein Gegenstand aus grosser Distanz gesehen erscheint uns kleiner als bei nahem Betrachtungsabstand. Oder anders gesagt: Von zwei gleich grossen Gegenständen erscheint uns der näher liegende grösser. Bei Betrachtung unserer beiden Schuhe aus naher Distanz ist die Entfernung Auge erster Schuh viel kleiner als derjenige vom Auge zum zweiten Schuh. Die Proportionen beider Schuhe sind daher sehr unterschiedlich. Betrachten wir das Sujet dagegen aus grosser Distanz, ist das Entfernungsverhältnis nahezu gleich geworden.

Dass wir im ersten Fall eine kurze Brennweite zur Aufnahme verwenden, im zweiten aber eine lange, ist auch hier lediglich eine Folge der Forderung nach Formatfüllung.

 

Beeinflussung der Perspektive

Zur zweidimensionalen Darstellung der dritten Dimension Tiefe verwenden wir Fluchtlinien. Eine Beeinflussung ist lediglich durch unterschiedliche Aufnahmedistanzen möglich. Zur Wiedergabe der Höhe sind in den meisten Fällen Fluchtlinien der Senkrechten unerwünscht.

Beim formatfüllenden Fotografieren eines Hauses mit einer starren Kamera kommt es oft vor, dass man die Kamera mehr oder weniger stark nach oben schwenken muss und somit die Lage des Films oder Chips nicht mehr parallel zu den Senkrechten des Bauwerks steht. Das Dach des Hauses ist wesentlich weiter entfernt als die Grundmauern und wird dadurch kleiner dargestellt. Das Bauwerk verjüngt sich nach oben und es neigt sich optisch nach hinten; es sind stürzende Linien entstanden, die in einigen Fällen – wenn stark übertrieben, siehe Titelbild zu dieser Folge – den Eindruck schwindelnder Höhe wirkungsvoll unterstützen. In vielen Fällen ist diese nichtrealistische Perspektive jedoch unerwünscht.

Stellt man bei gleichem Standpunkt die Kamera gerade, ist sehr viel Boden und nicht das ganze Haus abgebildet. Mit einer starren Kamera ist das Problem lösbar, indem man die Aufnahmedistanz so weit vergrössert, bis auch bei gerade gehaltener Kamera das ganze Bauwerk abgebildet wird. Lassen Sie sich nicht stören, wenn jetzt das halbe Bildformat nur Boden zeigt; in den meisten Fällen lässt sich das durch nachträgliche Ausschnittvergrösserung wieder wettmachen.

 

links: Stürzende Linien infolge Schräghalten der Kamera
rechts: Stürzende Linien bei der elektronischen Bildbearbeitung ausgeglichen

Bereits bei der Aufnahme sind stürzende Linien mit Hilfe einer verstellbaren Fachkamera oder in der Kleinbildfotografie mit einem Shift-Objektiv korrigierbar. Damit lässt sich mit paralleler Hochverschiebung der Objektivebene trotz gerade gehaltener Kamera der Ausgleich erzielen.

Mit dem Bildverarbeitungsprogramm z.B. Photoshop ist die Möglichkeit zur nachträglichen Korrektur ebenfalls gegeben. Allerdings darf man den Ausgleich nicht übertreiben. Steht ein Hochhaus nämlich absolut gerade, unterliegen wir einer optischen Täuschung. Unser Gehirn weiss vom Effekt der stürzenden Linien und korrigiert diese geringfügig. Präsentieren wir ihm ein hohes Gebäude mit völlig parallelen Senkrechten, korrigiert unser Gehirn und wir haben das Gefühl, das Gebäude laufe oben auseinander. Man sollte daher immer etwas unterkorrigieren und ein ganz geringes Zusammenlaufen der Senkrechten belassen.

 

Die allseitig verstellbare Fachkamera ermöglicht neben dem einfachen Geradestellen der Senkrechten noch eine weitere Beeinflussung der Perspektive. Da sich auch die Bildebene allseitig schwenken lässt und diese wie eine Projektionswand des als Projektor wirkenden Objektivs betrachtet werden kann, können die Fluchtlinien nahezu beliebig beeinflusst werden.

Als gelernter Fotograf hat man für Architekturaufnahmen immer eine Fachkamera verwendet, bei welcher sich die Objektivstandarte und die Bildstandarte gegenseitig verschieben lassen. Dadurch wurden parallele Senkrechten möglich und wir konnten groteske stürzende Linien von starren Kameras stammend als Schreckenskammern abtun. Als die ersten PC-Objektive zur Kleinbildkamera auf den Markt kamen, haben wir sie zuerst etwas belächelt wegen der vergleichsweise geringen Korrekturmöglichkeiten.

Und erst recht lachten wir als die Fotografie mit eigentlich fürs Telefonieren gedachten Geräten Allgemeingut wurde.

Zu Unrecht. Mit modernen Smartphones mit hochentwickelten Kameras und der entsprechenden App können auch Architekturaufnahmen mit Perspektivkorrektur in hoher Qualität erstellt werden. Eine dazu geeignete App ist unter anderen Gimbse Kamera (für iPhone oder iPad ab iOS 13.0 und auch Mac mit OS 11 und einem M1-Chip) mit eingebautem Perspektiv-Assistent des deutschen Entwicklers Christian Kappertz.

 

Betrachtungsperspektive

Mit der Gestaltung der Perspektive bei der Aufnahme sind die Möglichkeiten noch lange nicht ausgeschöpft. Auch das Verhältnis von Bildgrösse zu Betrachtungsabstand spielt eine nicht zu unterschätzende Rolle. Damit ein Bild genau so wirkt, wie der Fotograf es sich vorstellt, sollte es normalerweise unter einem Betrachtungswinkel angesehen werden, der dem Aufnahmewinkel entspricht.

Dieses Repetitorium beispielsweise betrachten Sie aus der normalen Lesedistanz von rund 30 bis 40 cm. Ich müsste also die Grösse aller publizierten Bilder so wählen, dass diesen Verhältnissen Rechnung getragen wird. Leider ist das in vielen Fällen gar nicht möglich und manchmal ist die bewusste Missachtung der Regel sogar erwünscht um einen zusätzlichen Bildeffekt zu erzeugen. Sehr oft ist dies der Fall, wenn man mit einem sogenannten Fisheye-Objektiv fotografiert und mit diesem naturgemäss sehr nah ans Objekt herangeht.

Das obige Bild des Schulbusses ist mit dem Canon Fisheye 1:2,8/15 mm entstanden und zeigt die typischen Fisheye-Verzeichnungen. Allerdings stammt die rundliche Verzeichnung eigentlich gar nicht vom Fisheye-Objektiv (es handelt sich bei diesem Objektiv ja um ein nichtverzeichnendes Vollformat-Fisheye), sondern vom starken Missverhältnis zwischen der sehr kurzen Aufnahmedistanz und dem nunmehr viel zu grossen Betrachtungsabstand. Um einen unverzeichneten Bildeindruck zu erhalten, muss folgendes Verhältnis übereinstimmen:

Aufnahmedistanz : Gegenstandsgrösse = Bildbetrachtungsdistanz : Bildgrösse.

Wenn Sie beim Betrachten des obigen Bildes die eigentlich notwendige Betrachtungsdistanz einhalten wollen, müssten Sie das Bild aus einer Distanz von wenigen Zentimetern betrachten, was Sie mit einer Lupe machen sollten. Schielen Sie bei dieser Betrachtungsweise gegen die Ecken des Bildes, sind die perspektivischen Verzeichnungen wie durch ein Wunder verschwunden!

© by Jost J. Marchesi

In der 5. Folge am nächsten Freitag geht es um Schärfe und Unschärfe.

 

Lesen Sie auch

Folge 1: «Licht, das «Rohmaterial» der Fotografie» (28.05.2021)
Folge 2: «Lichtausbreitung, Reflexion und Absorption» (04.06.2021)
Folge 3: «Wie das Licht gebrochen wird» (11.06.2021)