Herkömmliche Weitwinkelobjektive von analogen Kameras können beim Einsatz in Digitalkameras zu Artefakten und zusätzlicher Vignettierung im Randbereich führen. Das (unkorrigierte) Titelbild zu dieser Folge beweist, dass dies nicht unbedingt der Fall sein muss, wenn es sich um ein qualitativ hochwertiges Objektiv handelt und der Bildwinkel grösser ist als für das Sensorformat notwendig. Aufnahme: ilka Marchesi
Die in der Fotografie verwendeten Bildformate sind normalerweise rechteckig. Es ist uns deshalb nicht unbedingt bewusst, dass Objektive eigentlich runde Bilder entwerfen, aus denen unser Aufnahmeformat einen entsprechenden Teil herausschneidet. Hersteller von starren Kleinbild-Systemkameras sprechen in ihren Objektiv-Datenblättern meistens von Bildwinkel, meinen damit jedoch nicht Bildwinkel, sondern Formatwinkel oder genauer, doppelter Feldwinkel. Die vorliegende Lektion bringt Klarheit in den Begriffswirrwarr.
Bildwinkel
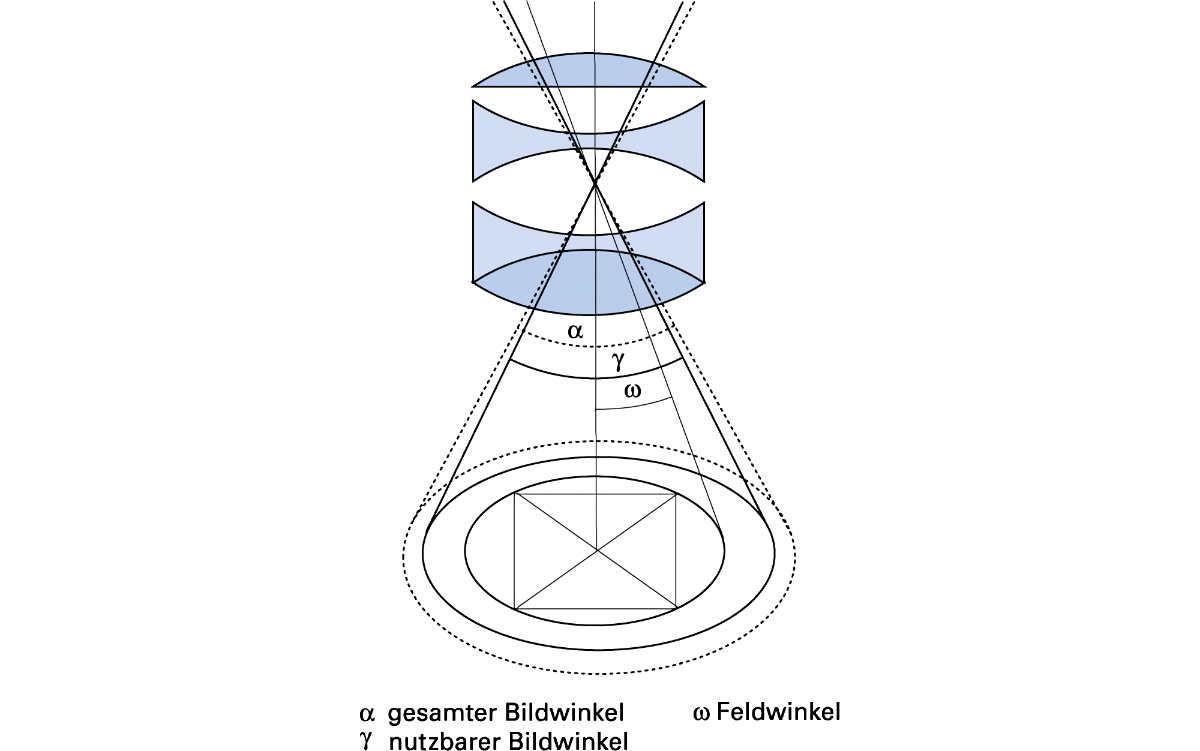
Ein Objektiv entwirft ein rundes Bild, das einen gewissen Ausschnitt der Gegenstandsebene darstellt. Bringt man das Objektiv an einer grösseren Kamera als vorgesehen an und stellt auf Unendlich (∞) scharf, so zeichnet sich auf der Mattscheibe ein kreisrundes Bild ab, das gegen den Rand hin unschärfer und lichtschwächer wird.
Der Bildkreis
Begriffe zum Bildwinkel
Den Winkel über dem gesamten Bildkreis (α) – vom Mittelpunkt des Objektivs aus gesehen – bezeichnet man als gesamten Bildwinkel. Innerhalb des gesamten Bildwinkels befindet sich ein etwas kleinerer Bereich, der eine für die Praxis noch genügende Abbildungsqualität liefert. Er ist der brauchbare Bildwinkel oder kurz Bildwinkel (γ). Seine Grösse ist in den technischen Datenblättern der Grossformat-Objektivhersteller angegeben und hängt unter anderem davon ab, welche Anforderung man an die Abbildungsqualität stellen muss. Beim Abblenden des Objektivs wird der brauchbare Bildwinkel, und damit der Bildkreis, durch Milderung der optischen Randfehler in der Regel etwas grösser.
Den für ein bestimmtes Negativformat schliesslich ausgenützten Bildwinkel bezeichnet man als doppelten Feldwinkel (2ω). Der Feldwinkel wird über die Formatdiagonale von Formatmitte bis Formatecke gemessen. Der doppelte Feldwinkel (auch Formatwinkel genannt) wird in den Katalogen der Objektivhersteller angegeben, die Objektive für starre Klein- und Mittelformatkameras anbieten. Meistens wird dort aus Unwissenheit vom Bildwinkel gesprochen; gemeint ist aber der Formatwinkel.
Der Bildwinkel ist – im Gegensatz zum doppelten Feldwinkel (Formatwinkel) – nicht etwa von der Brennweite, sondern allein und einzig von der Konstruktionsart des Objektivs (Objektivtypus) abhängig. Das bedeutet nichts anderes, als dass ein bestimmter Objektivtypus einen ganz bestimmten Bildwinkel besitzt, der typisch für seine Konstruktionsart ist.
Um einen bestimmten Objektivtypus für ein bestimmtes Aufnahmeformat verwenden zu können, muss dieser einen Bildwinkel besitzen, der mindestens gleich gross ist wie der vom eigentlichen Aufnahmeformat ausgenutzte doppelte Feldwinkel. Im Gegensatz zu starren Kleinformatkameras benutzen bewegliche Grossformatkameras Objektive, die möglichst grosse Bildwinkel besitzen, damit Formatverschiebungen innerhalb des Bildkreises möglich werden. Dort werden drei Grundtypen mit folgenden Bildwinkeln verwendet:
Bildwinkel für Grossformatobjektive:
Repro-Objektive: ca. 50°
Normalobjektive: ca. 70°
Weitwinkelobjektive: ca. 100° – 105°
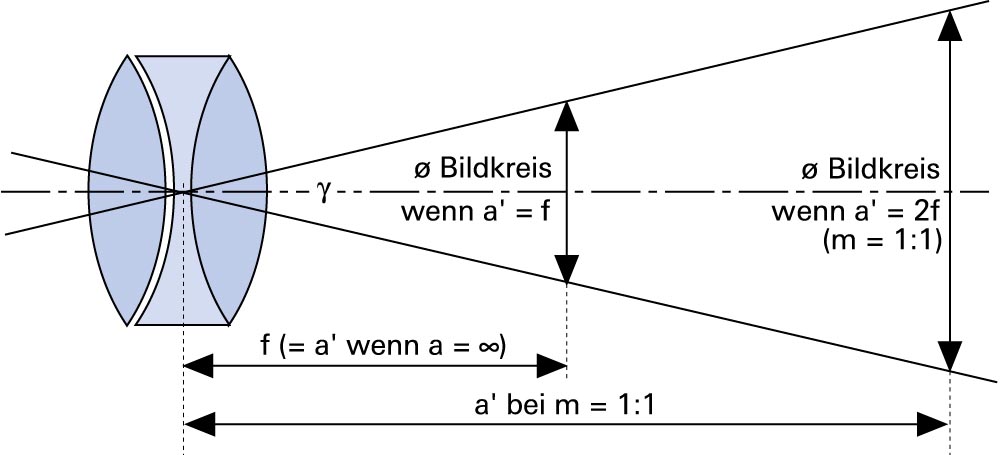
Bei gleichbleibendem Bildwinkel verändert sich die Bildkreisgrösse in Abhängigkeit der Brennweite bzw. des Kameraauszugs.
Bildkreis
Bei gleichbleibendem Bildwinkel vergrössert sich der auf der Bildebene gebildete Bildkreis mit zunehmendem Kameraauszug. Das bedeutet, dass bei gleichem Objektivtypus der Bildkreis bei längerer Brennweite entsprechend grösser wird, ebenso natürlich bei zunehmendem Abbildungsmassstab, denn dann wird ja der Kameraauszug ebenfalls länger.
Diese Überlegungen sind vor allem in der Grossformatfotografie von Bedeutung. Verwendet man nämlich ein Objektiv der Brennweite 180 mm, ist bei normalkonstruierten Objektiven der Bildkreis bei Scharfeinstellung auf ∞ gerade so gross, dass das Aufnahmeformat 13 x 18 cm ausgezeichnet wird. Irgendwelche Verschiebungen der optischen Achse – Verschiebungen der Objektivebene gegenüber der Bildebene, eine Technik, die für viele Zwecke in der Berufsfotografie notwendig ist – sind dann nicht mehr möglich. Im Aufnahme-Nahbereich dagegen verlängert sich der Kameraauszug a‘, und der Bildkreis wird entsprechend grösser. In diesem Fall lässt sich das Negativformat innerhalb des gewachsenen Bildkreises wieder etwas verschieben.
Der effektive und nutzbare Bildkreisdurchmesser dBK lässt sich leicht errechnen, wenn Bildwinkel und Kameraauszug bekannt sind:
In den technischen Datenblättern der Grossformatobjektive beziehen sich Bildkreisdurchmesser in der Regel auf Unendlicheinstellung und auf Abblendung 22.
Natürlich müssen auch Tilt- und Shift-Objektive (siehe Folge 7) einen möglichst grossen Bildkreis aufweisen, der das Aufnahmeformat um soviel überragt, dass eine vernünftige Verschiebung und Schwenkung möglich wird.
Auch in der Labortechnik ist dieser Tatsache ebenfalls eine gewisse Bedeutung zuzuordnen: Beim Vergrössern arbeitet man üblicherweise mit Objektiven, die einen Bildwinkel von rund 50° aufweisen. Um damit das Negativformat genügend auszuzeichnen, sind bestimmte Minimalbrennweiten erforderlich:
24 x 36 mm f = 50 mm
6 x 6 cm f = 80 mm
6 x 9 cm f = 105 mm
4 x 5 inch f = 150 mm
13 x 18 cm f = 240 mm
8 x 10 inch f = 300 mm
Will man ein 6 x 9 cm grosses Negativ statt zu vergrössern, um einen bestimmten Faktor verkleinern, wird der Auszug an dem Vergrösserungsgerät entsprechend länger, manchmal so lang, dass eine Scharfeinstellung – konstruktiv bedingt – nicht mehr möglich ist. In solchen Fällen kann man auf das kürzerbrennweitige Objektiv 80 mm oder gar 50 mm ausweichen, obwohl das Negativformat 6 x 9 cm beträgt. Denn bei dem notwendigen längeren Objektivauszug wird (bei gleichbleibendem Bildwinkel) der Bildkreis grösser. Je nach Abbildungsmassstab zeichnet er jetzt das bedeutend grössere Negativformat ohne Schärfeabfall und Vignettierung aus.
Brennweite und Bildformat
Die Bezeichnungen «kurze», «normale» oder «lange» Brennweite sind relativ und beziehen sich allein auf das Negativ- bzw. Sensorformat. Langbrennweitige Objektive erzeugen grössere Bilder als kurzbrennweitige. Bei gleichbleibendem Aufnahmeformat entsprechen die durch langbrennweitige Objektive erzeugten Bilder einem entsprechend stärkeren Ausschnitt.
Als «normal» wird eine Brennweite bezeichnet, die etwa der Formatdiagonalen entspricht. Als «kurze» Brennweite gilt die Länge der grösseren Formatseite oder kürzer, und als «lang» bezeichnet man solche, die mindestens so lang sind wie die doppelte längere Formatseite.
24 x 36 mm 4 x 5 inch
kurz 35 mm 90 mm
normal 50 mm 150 mm
lang 90 mm 240 mm
Für Nicht-Vollformat-Sensoren, welche kleiner als 24 x 36 mm sind, gelten die um den betreffenden Crop-Faktor verkleinerten Brennweiten (für APS-C Crop-Faktor 1,5 bis 1,6)
Diese Beispiele demonstrieren folgende Zusammenhänge: Bildet man einen Gegenstand mit der Objektivbrennweite 50 mm auf das Kleinbild-Vollformat 24 x 36 mm formatfüllend ab, wird dieser aus derselben Aufnahmedistanz auch auf das Format 4 x 5 inch formatfüllend, sofern man dort ein Objektiv der Brennweite 150 mm verwendet. Die gleichen Verhältnisse treten beim APS-C Format ein (Canon 22,2 x 15 mm) beim Verwenden der Brennweite 30 mm.
Zwischen Brennweite und doppeltem Feldwinkel (2ω) besteht ungefähr folgender Zusammenhang:
Brennweite wie Formatwinkel
kurze Formatseite ~ 80°
lange Formatseite ~ 64°
Formatdiagonale ~ 53°
doppelte kurze Formatseite ~ 45°
doppelte lange Formatseite ~ 35°
Anders gesagt: Entspricht die Länge der verwendeten Objektivbrennweite einer bestimmten Strecke des Aufnahmeformats, entsteht bei einem anderen Aufnahmeformat ein identischer Bildausschnitt, sofern die Brennweite bei jenem Format der gleichen charakteristischen Formatstrecke entspricht. Weiss man beispielsweise aus Erfahrung wie gross der Bildausschnitt beim Kleinbildformat mit einem 24-mm-Objektiv ist (kurze Formatseite beim Kleinbild), kann man ableiten, dass bei Verwendung des Aufnahmeformats 4 x 5 inch mit einem 90- bis 100-mm-Objektiv (kurze Formatseite beim Format 4 x 5 inch) derselbe Bildausschnitt entsteht. Adäquat dazu entsteht beim Format APS-C ein gleicher Bildausschnitt mit dem 15 mm Objektiv.
Für starre Kameras (Kleinbild- und Mittelformatkameras) sind Objektive mit folgenden doppelten Feldwinkeln (Formatwinkel) üblich:
Fernobjektive, Teleobjektive: < 20°
Langbrennweitige Objektive: 20 – 40°
Normalobjektive: 40 – 55°
Weitwinkelobjektive: > 55°
Fisheye-Objektive: bis über 180°
Brennweitenvergleich bei Digitalkameras
Die meisten Digitalkameras besitzen Aufnahme-Chips, die kleiner als das übliche Kleinbildformat 24 x 36 mm sind. Bei Verwendung eines Objektivs gleicher Brennweite entsteht dadurch ein engerer Bildausschnitt. Oder anders gesagt: Setzt man eine Digitalkamera ein, welche keinen Vollformat-Chip verwendet, müssen für das Erzielen gleicher Ausschnitte wie in der Kleinbildfotografie entsprechend kürzere Objektivbrennweiten verwendet werden. Die Kamerahersteller geben in ihren Datenblättern für den Vergleich den sogenannten Crop-Faktor an (von crop = beschneiden).
Der APS-C-Chip bei Canon-Kameras beispielsweise hat die Grösse 22,5 x 15 mm. Im technischen Datenblatt ist unter «Brennweite» der Faktor 1,6 angegeben. Dies bedeutet, dass das Aufnahmeformat linear um den Faktor 1,6 kleiner ist als das Kleinbildformat und für gleiche Bildausschnitte demzufolge Objektive mit 1,6-mal kürzerer Brennweite verwendet werden müssen. Ein bereits bestehendes Weitwinkelobjektiv mit der Brennweite 24 mm hat somit einen Bildausschnitt zur Folge wie ein Objektiv mit Brennweite 38 mm an einer Vollformat-Kamera.
Perspektive
Die Perspektive ist absolut unabhängig von der Brennweite! Wenn vom gleichen Standort aus Aufnahmen mit verschiedenen Brennweiten gemacht werden, so zeigen alle Aufnahmen dieselbe Perspektive unabhängig von der Brennweite. Unterschiedlich ist lediglich der Formatwinkel und dadurch der Bildausschnitt.
Die Perspektive ist (neben projektiven Beeinflussungen beim Schwenken der Bildebene mit Fachkameras oder Kameras mit Tilt-Objektiven) allein und einzig vom Aufnahmestandort abhängig! Kurze Aufnahmedistanzen führen zu starker Konvergenz der Fluchtlinien, was eine übertriebene Perspektive ergeben kann. Lange Aufnahmedistanzen dagegen erzeugen eine flachere Perspektive. Dass für den ersterwähnten Fall meistens ein kurzbrennweitiges und im zweiten Fall ein langbrennweitiges Objektiv verwendet wird, ist lediglich eine Folge des gewünschten Bildausschnitts und nicht etwa die Ursache für eine andere Perspektive. Vermeiden Sie daher verwirrliche und nicht existente Bezeichnungen wie «Weitwinkelperspektive» oder «Teleperspektive».
Ausführlichere Hinweise zum Begriff der Perspektive finden Sie in Folge 4.
Vignettierung (Randhelligkeitsabfall)
Die Lichtstärke eines Objektivs ist als rein geometrisches Öffnungsverhältnis angegeben (siehe Folge 7). Wieviel Licht aber tatsächlich auf den Film fällt, ist unter anderem auch davon abhängig, in welchem Winkel ein Lichtbündel auf das Objektiv fällt.
Natürliche Vignettierung
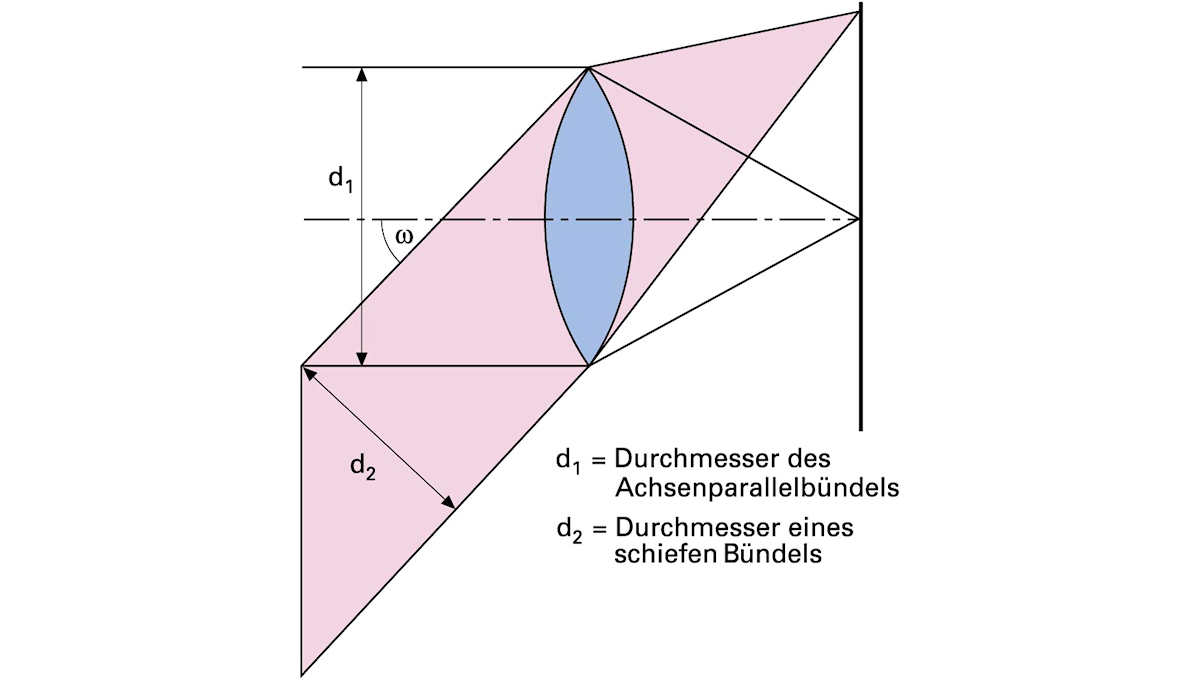
Das geometrische Öffnungsverhältnis hat nur Gültigkeit für die Bildmitte. Am Objektrand liegende Gegenstandspunkte senden ein Lichtbündel aus, das den Glaskomplex des Objektivs schräg passiert. Aus rein geometrischen Gründen ist der Durchmesser eines solchen schiefen Bündels geringer und vom einfallenden Winkel abhängig. Dadurch kann ein Gegenstandspunkt am Bildrand merklich weniger Licht durch den Komplex senden als ein gleich heller Punkt in der Bildmitte. Dadurch entsteht ein kontinuierlicher Helligkeitsabfall, ausgehend von der Bildmitte in Richtung Bildecken.
Berechnung des Helligkeitsabfalls
Dieser Randhelligkeitsabfall lässt sich als Funktion des Einfallswinkels und aus dem ausgenutzten doppelten Feldwinkel (Formatwinkel) des Objektivs nach dem sogenannten Cosinus-hoch-vier-Gesetz berechnen.
Dabei ist:
Eω = Beleuchtungsstärke unter Winkel ω
E0 = Beleuchtungsstärke in der Bildmitte
ω = Feldwinkel oder halber Formatwinkel
Beispiel 1
Das 50-mm-Objektiv an einer Vollformat-Kamera weist einen doppelten Feldwinkel von 45° auf. Die Beleuchtungsstärke in der Bildmitte beträgt 100 lx. Wie gross ist die wirksame Beleuchtungsstärke am Bildrand? Wieviel macht dieser Randhelligkeitsabfall in Blendenwerten aus?
Eω = 100 • (cos 22,5°)4 = 72 lx – dies entspricht einer Helligkeitsabnahme zum Bildrand von ~ 1/2 Blende.
Beispiel 2
Das Objektiv 65 mm an einer 4 x 5 inch-Kamera weist einen doppelten Feldwinkel von 100° auf. Die Beleuchtungsstärke in der Bildmitte beträgt 100 lx. Wie gross ist die Beleuchtungsstärke am Bildrand? Wieviel macht dieser Helligkeitsabfall in Blendenwerten aus?
Eω = 100 • (cos 50°)4 = 17 lx – dies entspricht einer Helligkeitsabnahme zum Bildrand von ~ 2,5 Blenden.
Korrekturmöglichkeit
Die natürliche Vignettierung ist kein Abbildungsfehler. Vielmehr ist sie rein geometrisch bedingt und tritt bei jedem Objektiv auf. Störend wirkt sich dieser Randhelligkeitsabfall in der analogen Fotografie aber nur aus, wenn er mehr als zwei Blendenwerte beträgt, was nur bei extremen Weitwinkelobjektiven der Fall ist. Eine Korrektur ist lediglich durch die Verwendung eines konzentrischen Verlauffilters möglich.
Konzentrischer Verlauffilter
Es handelt sich dabei um einen präzis, planparallel geschliffenen Filter mit einem von innen nach aussen verlaufenden neutralgrauen Belag. Konzentrische Verlauffilter sind nur für die Weitwinkelobjektive der Grossformat-Fachkameras lieferbar und innerhalb der Mittel- und Kleinformatfotografie unbekannt.
Durch Abblenden kann die natürliche Vignettierung nicht gemildert werden!
In der digitalen Fotografie dagegen lässt sich der Randhelligkeitsabfall durch das Bildbearbeitungsprogramm elegant beheben.
Künstliche Vignettierung
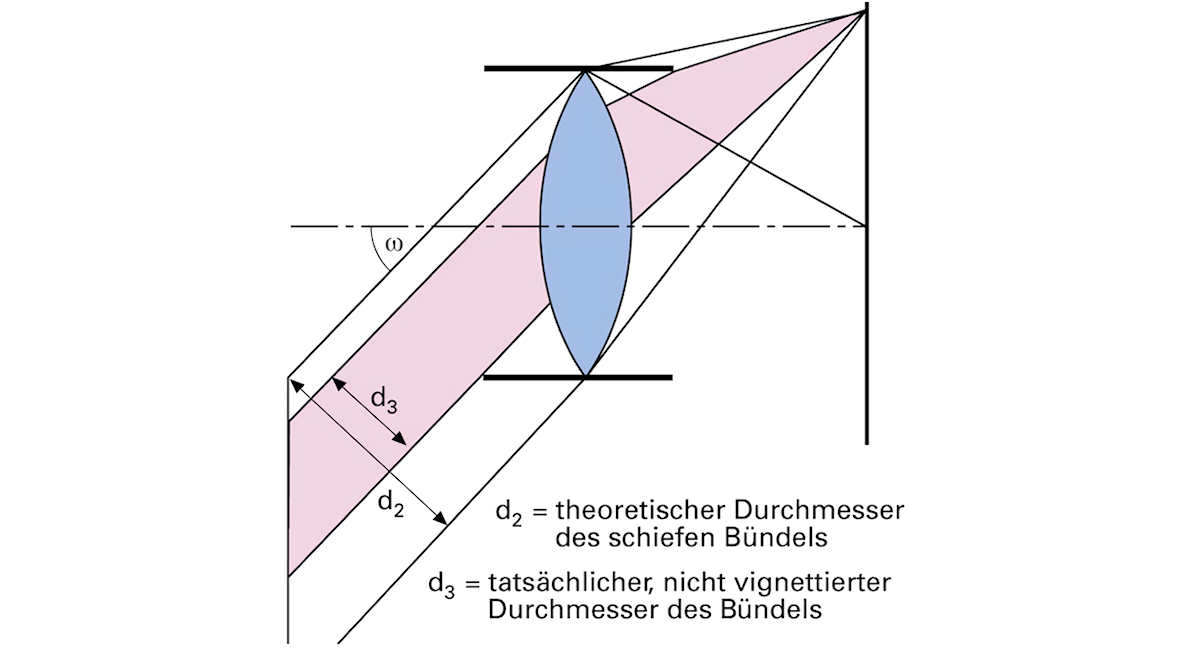
Da ein Objektiv nicht aus einer einzelnen, freistehenden Linse besteht, sondern eine komplizierte Kombination vieler mechanisch gefasster Glaslinsen ist, entsteht bei schief einfallenden Bündeln noch eine weitere Verschlechterung. Bedingt durch die Objektivfassung, wird ein beträchtlicher Teil des schiefen Bündels, das bereits aus geometrischen Gründen einen geringeren Durchmesser aufweist als ein achsenparalleles Bündel, noch zusätzlich durch die Fassungsteile beschnitten.
Künstliche Vignettierung
Die künstliche Vignettierung lässt sich durch Abblenden mildern und beheben.
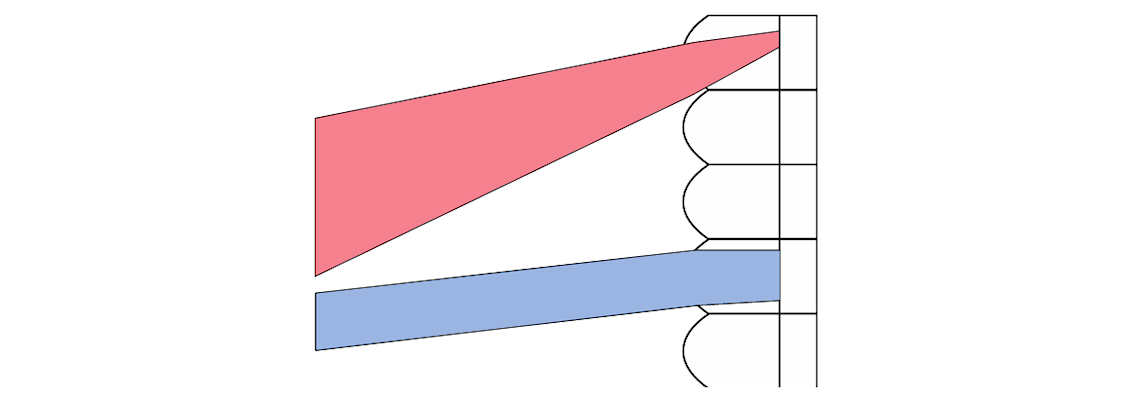
Die Verhältnisse lassen sich an einem beliebigen Objektiv studieren, wie es nachstehende Abbildungsserie demonstriert: Schaut man genau entlang der Achse auf ein nicht abgeblendetes Objektiv und simuliert damit ein Strahlenbündel, das genau parallel der Achse einfällt, so erkennt man die gesamte Objektivöffnung unbeschnitten als vollen Kreis. Dreht man hingegen das Objektiv etwas und simuliert dadurch den Weg eines schief einfallenden Bündels, so erkennt man als Objektivöffnung nur noch ein Kreiszweieck mit merklich kleinerer Fläche. Die Fassungsteile schneiden einen Teil des Bündels ab. Blendet man bei gleicher Betrachtungslage aber langsam ab, so erkennt man früher oder später wieder die gesamte kreisrunde Blendenöffnung.
Darstellung der künstlichen Vignettierung:
links: Achsenparallelbündel bei offener Blende.
mitte: Schiefes Bündel bei offener Blende.
rechts: Schiefes Bündel bei Abblendung.
Die künstliche Vignettierung ist bei grösster Blendenöffnung am stärksten. Mit zunehmender Abblendung wird sie geringer, bis sie schliesslich überhaupt nicht mehr zur Geltung kommt. Es liegt in der Kunst des Objektivkonstrukteurs, die künstliche Vignettierung schon nach möglichst geringfügiger Abblendung zu beheben. Baut man beispielsweise die Vorder- und die Hinterlinsen grösser als für den Durchtritt des Achsenparallelbündels notwendig wäre, werden die zu den Bildecken hin zielenden Strahlen bedeutend weniger beschnitten.
Wie wir in dieser Lektion noch sehen werden, spielt die Vignettierung in der digitalen Fotografie noch eine weitere Rolle infolge der zusätzlichen Abschwächung von schief eintretenden Strahlen an den Randpixeln eines Bildempfangssensors.
Digitalobjektive?
Digitalkameras – sofern sie Aufnahme-Chips verwenden, die kleiner sind als die für das betreffende Kameramodell in der analogen Fotografie üblichen Filmformate – benötigen entsprechend kürzerbrennweitige Objektive. So enthalten die unzähligen Sucherkameras mit 11⁄8 Zoll Sensoren oft Varioobjektive mit dem Brennweitenbereich von 7,4 bis 22,4 mm (Canon Ixus 500, 3-fach-Zoom) oder 4,3 bis 43 mm (Canon Ixus 190, 10-fach-Zoom), was auf Kleinbild umgerechnet einem Brennweitenbereich von 36 bis 108 mm bzw. 21 x 207 mm entspricht. Es ist selbstverständlich, dass für diese Kameras die Vario-Objektive entsprechend der recht kurzen Brennweiten speziell gerechnet und an die besonderen Begebenheiten der kleinen Aufnahme-Chips angepasst sind.
An Kleinbildsystemkameras mit Vollformatsensoren oder solchen, die kleiner sind als das übliche Kleinbildformat (zum Beispiel Halbformat 24 x 16 mm oder APS-C-Format 22 x 15 mm) kann man behelfsmässig die herkömmlichen Objektive verwenden. Der Vorteil von Systemkameras ist ja, dass man beim Wechsel von der analogen zur digitalen Fotografie lediglich das Kamerabody neu kaufen musste und die vorher verwendeten Objektive solange weiterverwenden konnte, bis das Budget den Kauf neu berechneter Objektive ermöglicht.
Zu diskutieren ist, ob damit eine genügende Bildqualität zu erreichen ist oder ob man besser neue, für das kleinere Aufnahmeformat oder die speziellen Belange der digititalen Fotografie gerechneten Objektive anschaffen soll.
Retrofokus und Bildwinkel
Digital-Spiegelreflexkameras mit Nicht-Vollformatsensoren können im Gegensatz zu solchen für das volle Kleinbildformat mit einem merklich kleineren Schwingspiegel ausgerüstet sein und Objektive mit geringerem Bildwinkel verwenden. Wegen des kleineren Schwingspiegels kann die Hinterlinse des Objektivs näher am Sensor liegen und muss weniger stark retrofokal gebaut sein, wie bei Objektiven für Vollformatkameras (siehe Folge 7). Gleiches gilt für spiegellose Vollformat-Kameras. Das ist ein klarer Bauvorteil, ist doch die Korrektur aller optischer Fehler bei sehr kurzbrennweitigen Objektiven ausserordentlich aufwändig und teuer. Die Korrektur ist bei stark retrofokalen Systemen noch aufwändiger und das schlägt sich ganz klar in einem relativ hohen Preis nieder.
Darf der ausnutzbare Bildwinkel kleiner sein als bei Vollformatkameras, kann sich dies bezüglich optischer Korrektur gerade noch einmal positiv auswirken. Schwierig ist die Korrektur nämlich nicht in der Bildmitte, sondern vor allem gegen den Rand des Bildwinkels zu. Kann dieser kleiner gehalten werden, ist die Gesamtkorrektur kompromissloser zu realisieren und man kann weniger stark brechende Gläser verwenden.
Ein typisches Objektiv dieser Art ist beispielsweise das sehr kompakte, leichte und preisgünstige Objektiv Canon EF-S 18 – 55 mm, das auf die kleinere Sensorgrösse abgestimmt ist. Das «S» in der Objektivbezeichnung steht für «Short back focus». Mit Ausnahme der deutlichen Verzeichnung in den extremen Brennweitenstellungen weist das Objektiv einen wirklich ausgezeichneten Korrekturzustand auf. Wegen dem geringeren Bildwinkel kann es jedoch nicht auf Vollformatkameras eingesetzt werden. Andere Objektive mit reduziertem Bildwinkel sind beispielsweise das Canon EF-S 10 – 22 mm und das Makro-Objektiv Canon EF-S 2,8/60 mm USM, das ohne Zubehör den Abbildungsmassstab 1 : 1 erreicht. Bei Nikon heisst die entsprechende Objektivserie DX, bei Pentax DA und bei Sigma DC.
Bei den meisten Vario-Objektiven dieser Bauart zeigen sich die typischen Schwächen von Objektiven mit geringem Bildwinkel: Verstärkte Vignettierung und eine deutliche Verzeichnung im Weitwinkelbereich. Die Verlagerung der Hauptebene nach hinten führt bei kurzen Brennweiten dazu, dass Verschmutzungen wie Staubkörner oder Fusseln auf der Frontlinse je nach Blendeneinstellung erkennbar abgebildet werden.
Zur Korrektur von sphärischen Abbildungsfehlern enthalten diese Objektivtypen meistens ein bis zwei asphärische Linsenglieder, die aus Kostengründen häufig aus einem optischen Kunststoff gefertigt sind. Zusammen mit der Leichtbauweise sind dadurch Zentrierfehler bei der Fertigung der Objektive nicht immer auszuschliessen.
Objektivauflösung
Um die Frage zu beantworten, ob die Auflösung herkömmlicher Objektive aus der analogen Fotografie für den Einsatz in digitalen Spiegelreflexkameras genügend ist, müssen wir Auflösungsleistung der Objektive, Pixelgrösse beim Bildempfangssensor sowie Auflösungsvermögen von chemischem Filmmaterial miteinander vergleichen.
Wir gehen davon aus, dass hervorragende Spitzen-Objektive für den Kleinbildeinsatz bei Arbeitsblenden von 5,6 bis 8 ein Auflösungsvermögen von etwa 80 lp/mm (Linienpaaren pro Millimeter, das heisst je 80 weisse und schwarze Linien pro Millimeter) aufweisen. Diese Objektive können daher als kleinste Struktureinheit eine Linie mit der Dicke von 6,25 µm darstellen, denn 1000 : 160 ergibt 6,25.
Das ist und war absolut genügend für die analoge Fotografie. Es gab ausser im Microfilm-Bereich kein Filmmaterial, das diese Auflösung auch nur annähernd erreichte. Anders in der Digitalfotografie. Sind die einzelnen Pixel kleiner als 6 µm genügt das Auflösungsvermögen von 80 Lpmm nicht mehr.
Vollformat-Kameras mit 20 Megapixeln wie die Canon EOS-1D Marc III weisen gerade diese Pixel-Grenzgrösse auf.
Bei vielen höherauflösenden Systemen dagegen wird diese Grösse unterschritten. Solche Kameras benötigen Objektive mit noch höherer Auflösung. Nur gibt es die eben bisher nicht … Selbst das sagenumwobene Zeiss Otus 55 mm, das eine Auflösung bis 36 Megapixel bewältigen soll, muss bei einem Sensor mit 50 MP kapitulieren.
Bestehende Objektiv aus der analogen Fotografie können daher teilweise auch noch in der digitalen Fotografie brauchbar bleiben, sofern – bezogen auf das Vollformat – der Sensor in einer Grenzauflösung bis etwa 24 Megapixel bleibt.
Natürlich gilt diese Folgerung nur für qualitativ höchstwertige und daher teure Objektive! Preisgünstige Vario-Objektive lösen meistens nur etwa 40 lp/mm auf. Mit diesen ist bei kleiner Pixelgrösse keine maximale Bildqualität mehr möglich. Will oder muss man die Grenze von 24 MP übersteigen, bleibt als perfekte Lösung lediglich ein grösseres Sensorformat. Diese sind jedoch erheblich teurer und verlangen nach ebenfalls teuren Objektiven mit grösseren Bildwinkeln.
Das Randstrahlenproblem
Viel kritischer als die Auflösung der Objektive sind die Randstrahlenprobleme, vor allem bei sehr weitwinkligen Objektiven. Der elektronische Sensor stellt an den Strahlengang andere Ansprüche als der diesbezüglich gutmütige Film. Die Sensoroberfläche weist eine dreidimensionale Struktur auf mit meist erhöhten elektrischen Leiterbahnen zwischen den Pixeln, Mikrolinsen, Farbfilterchen und Antialiasing- sowie IR-Sperrfilter. Die Lichtstrahlen müssen diese Strukturen durchdringen, bevor sie endlich auf die lichtempfindliche Diode fallen. Für achszentrale Strahlen bergen diese Hindernisse keine Probleme, wohl aber für die extrem schräg einfallenden Strahlen, welche an den Bildrändern eine geringere Aktivität haben, wodurch die natürliche Vignettierung teils erheblich verstärkt werden kann. Durch Übergriffe auf benachbarte Pixel entstehen zudem Farbinterferenzen und Artefakte. Diese Effekte können – je nach Raffinesse des Rechenalgorithmus – die kamerainterne Bildaufbereitung (Antialiasing, Rauschunterdrückung usw.) nachhaltig stören. Im extremen Weitwinkelbereich bewirken schräg einfallende Strahlen neben der zusätzlichen Vignettierung oft einen starken Schärfeabfall sowie Farbveränderungen zum Rand hin. Ist der Farbquerfehler (Folge 9: Chromatische Aberration) nicht über das gesamte Bildfeld perfekt korrigiert, wirkt er sich am Bildrand, durch das Randstrahlenproblem unterstützt, erkennbar als Unschärfe aus.
Schräg einfallende Strahlenbündel erzeugen einen geringeren Diodenstrom, wodurch die natürliche Vignettierung der Objektive erheblich verstärkt wird. Die dadurch notwendige höhere Verstärkung des Fotostroms führt in den Randpartien zu verstärktem Bildrauschen.
Lösungsansätze
Lösungsansätze für das Randstrahlenproblem können am Rand angewinkelte Sensorelemente sein. Auch sogenannte BSI-Sensoren (hinterleuchtete CMOS-Sensoren) vermindern das Problem stark. BSI-Sensoren werden gleich wie andere Sensoren hergestellt. Sie werden jedoch umgedreht, abgeschliffen und so eingebaut, dass das Licht von der Rückseite her auf die lichtempfindlichen Elemente fallen kann. Die Ausleseschaltung stört dadurch nicht mehr und der Sensor kann bis doppelt so viel Licht auswerten. Gedanklich erfunden haben meine Studenten diese logische und naheliegende Möglichkeit bereits vor 20 Jahren. Doch bis zur Realisation kann so etwas dauern …
Andere Ansätze gehen von einer Software aus, welche im Bildaufbereitungs-Chip Störungen erkennen und diese algorithmisch beseitigen. Auch im Bildbearbeitungsprogramm lassen sich entsprechende Fehler wie Vignettierungen und chromatische Randaberration sowie kissenförmige oder tonnenförmige Verzeichnung korrigieren.
Nahezu telezentrisch
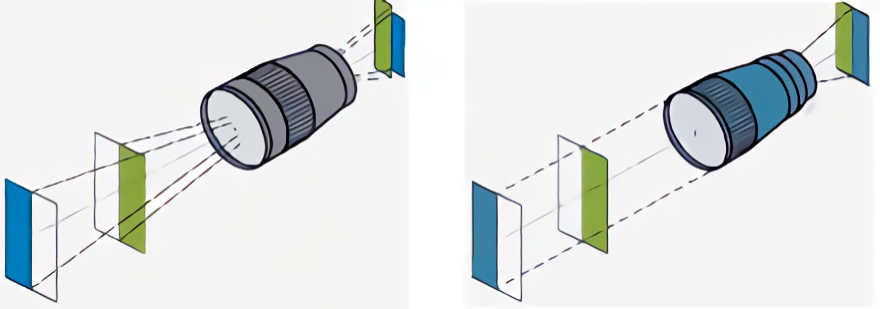
Die vielleicht optimalste Lösung wären Objektive mit einem ergo telezentrischen Strahlenverlauf. Telezentrische Objektive arbeiten mit parallelem Strahlengang. Dieser kleine Unterschied zu herkömmlichen Foto-Objektiven hat das berührungslose Messen, Prüfen und Erkennen von Körpern mittels CCD-Kameras revolutioniert. Weil sich im telezentrischen Gegenstandsraum selbst bei unterschiedlichen Objektentfernungen immer konstante Bildgrössen ergeben, beeinflussen Tiefenausdehnungen die Messungen nicht. Für übliche fotografische Aufnahmezwecke wären solche Objektive, welche nicht zentralperspektivisch arbeiten, unerwünscht. Kehrt man jedoch den Strahlengang um, so dass sich der parallele Strahlenverlauf statt im Gegenstands- im Bildraum befindet, gäbe es keine schräg einfallenden Randstrahlen; selbst die Pixel an den Bildecken würden von den Strahlen senkrecht getroffen.
links: Strahlenverlauf bei einem normalen Objektiv, rechts: Echter telezentrischer Strahlenverlauf
(Abbildungen: Zeiss)
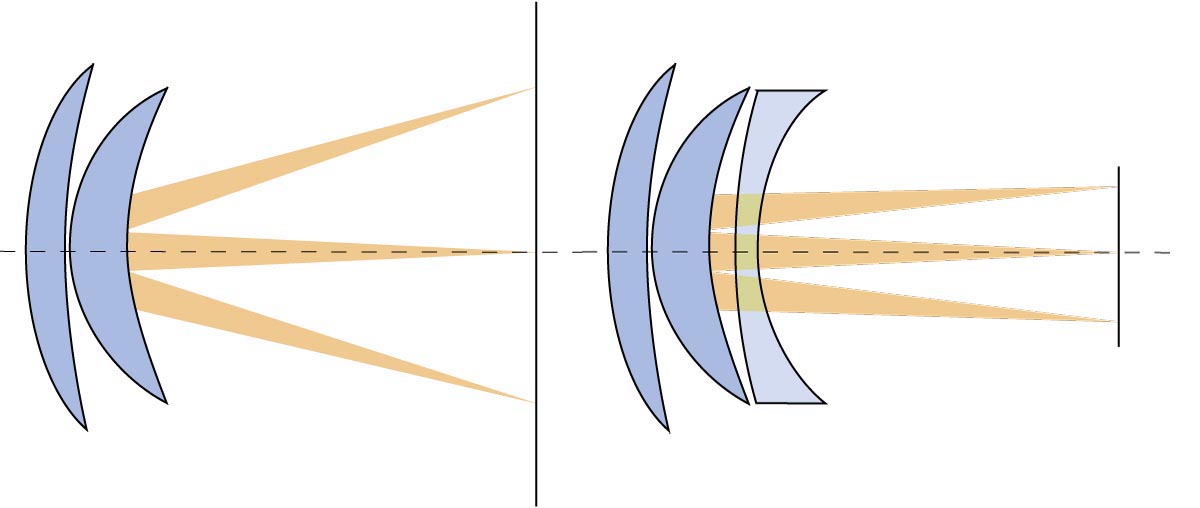
links: normaler Strahlenverlauf, rechts: «Nahezu telezentrischer» Strahlenverlauf
Ansätze in dieser Richtung sind bei einigen Herstellern von Digitalobjektiven wie Olympus (Zuiko Digitalobjektive) und den Digitalobjektiven von Schneider Kreuznach zu finden. Beide sprechen von «nahezu telezentrischem» Strahlenverlauf. Gelegentlich findet sich dafür auch der Ausdruck «ergo telezentrisch». Von besonderer Bedeutung ist dieser nahezu telezentrische Strahlenverlauf bei neuen sehr weitwinkligen Objektiven und relativ grossen Sensoren. Weniger wichtig beurteile ich das Problem bei nicht Vollformatsensoren, bei denen durchaus noch herkömmlichen Objektive eingesetzt werden können.
© by Jost J. Marchesi
In der 9. Folge am nächsten Freitag geht es um chromatische und sphärische Aberration.
Lesen Sie auch
Folge 1: «Licht, das «Rohmaterial» der Fotografie» (28.05.2021)
Folge 2: «Lichtausbreitung, Reflexion und Absorption» (04.06.2021)
Folge 3: «Wie das Licht gebrochen wird» (11.06.2021)
Folge 4: «Abbildungsverhältnisse und Perspektive» (18.06.2021)
Folge 5: «Schärfe und Unschärfe» (25. Juni 2021)
Folge 6: «Kanteneffekt, Streuung und Polarisation» (02.07.2021)
Folge 7: «Objektiv – das Auge der Kamera» (08.07.2021)







Klasse Beitrag, hätte ich vor einem Jahr gut gebrauchen können.
Besonders die 2. Abbildung hätte mir sehr geholfen!
Die Abbildung erklärt wie es zum Fokus-Beathing kommt und wie die „Vergrößerung“ bei Makro-Aufnahmen mit Zwischenringen zu erklären ist. Die Bildweite a‘ ist es mit der man rechnen muss und nicht mit der Brennweite, dann ist auch klar, warum man bei Makro-Aufnahmen viel eher in die Beugungsunschärfe kommt.
Mir ist der Zusammenhang zwischen Bildwinkel und Lichtstärke des Objektivs noch unklar. Die Lichtstärke errechnet sich aus effektiver Blendenöffnung und Brennweite. Ist also vom Bildwinkel unabhängig.
Nun besitzt ein MFT-Objektiv einen kleinen Bildkreis, ein KB-Objektiv einen größeren Bildkreis. Wenn beide Objektive nun die gleiche Brennweite und Blendenzahl haben, sollte doch die Anzahl der passierende Photonen gleich groß sein (Ich vermeide hier Bezeichnungen wie Lichtstärke). Allerdings würde ich erwarten, dass diese sich beim KB-Objektiv auf eine größere Fläche verteilen als bei MFT. Bedeutet dass, das der MFT-Sensor von einer höheren Photonendichte belichtet wird oder mache ich einen Denkfehler und die Photonendichte ist unabhängig vom Bildkreis?
Ich habe meinen Denkfehler selber erkannt. Der Bildkreis begrenzt ja nur das Abbild des Gegenstandes im Bildraum. Mit größerem Bildkreis vergrößert sich auch der Bildausschnitt aus dem Gegenstandsraum.
Übrigens: Eine großartige Serie. Vielen Dank!